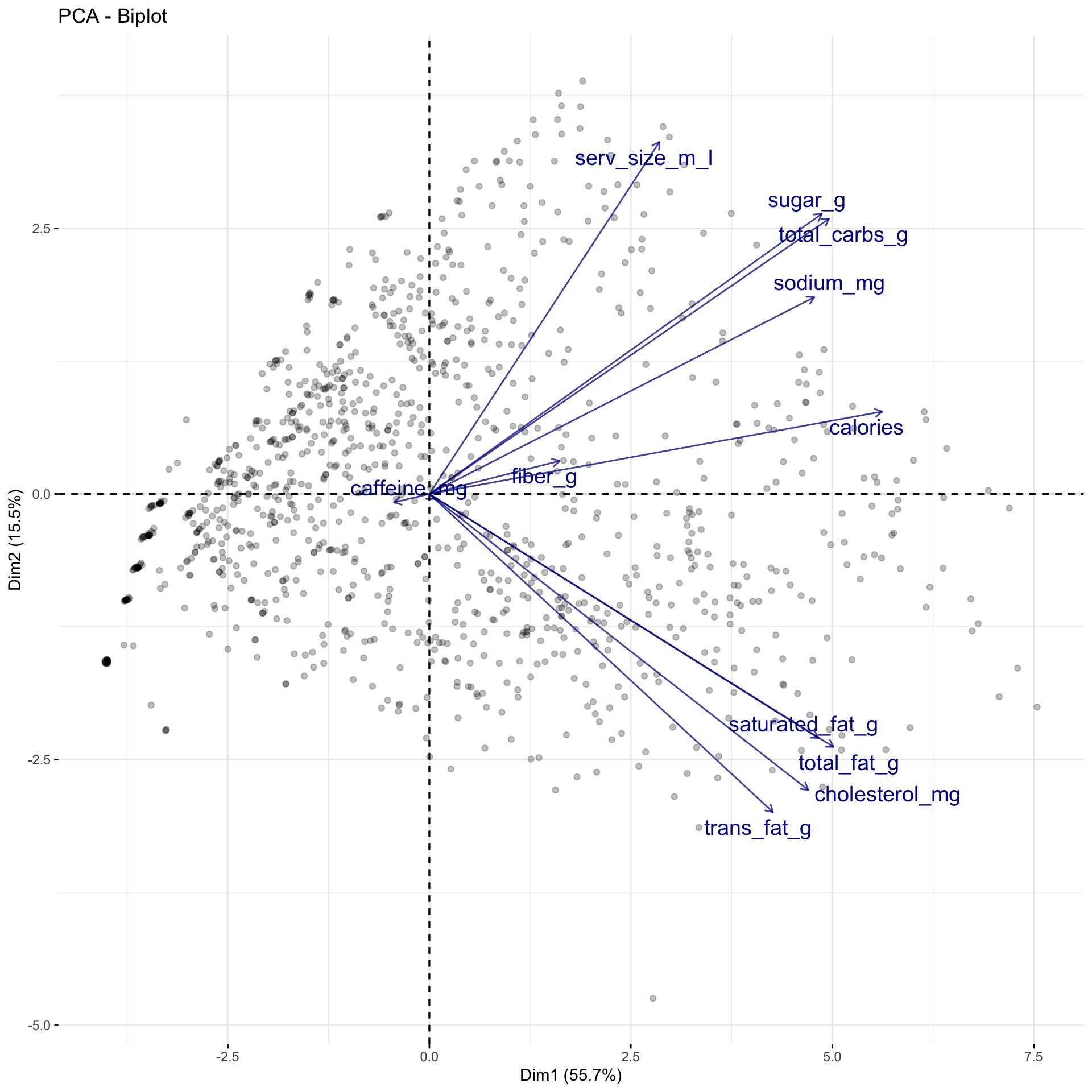
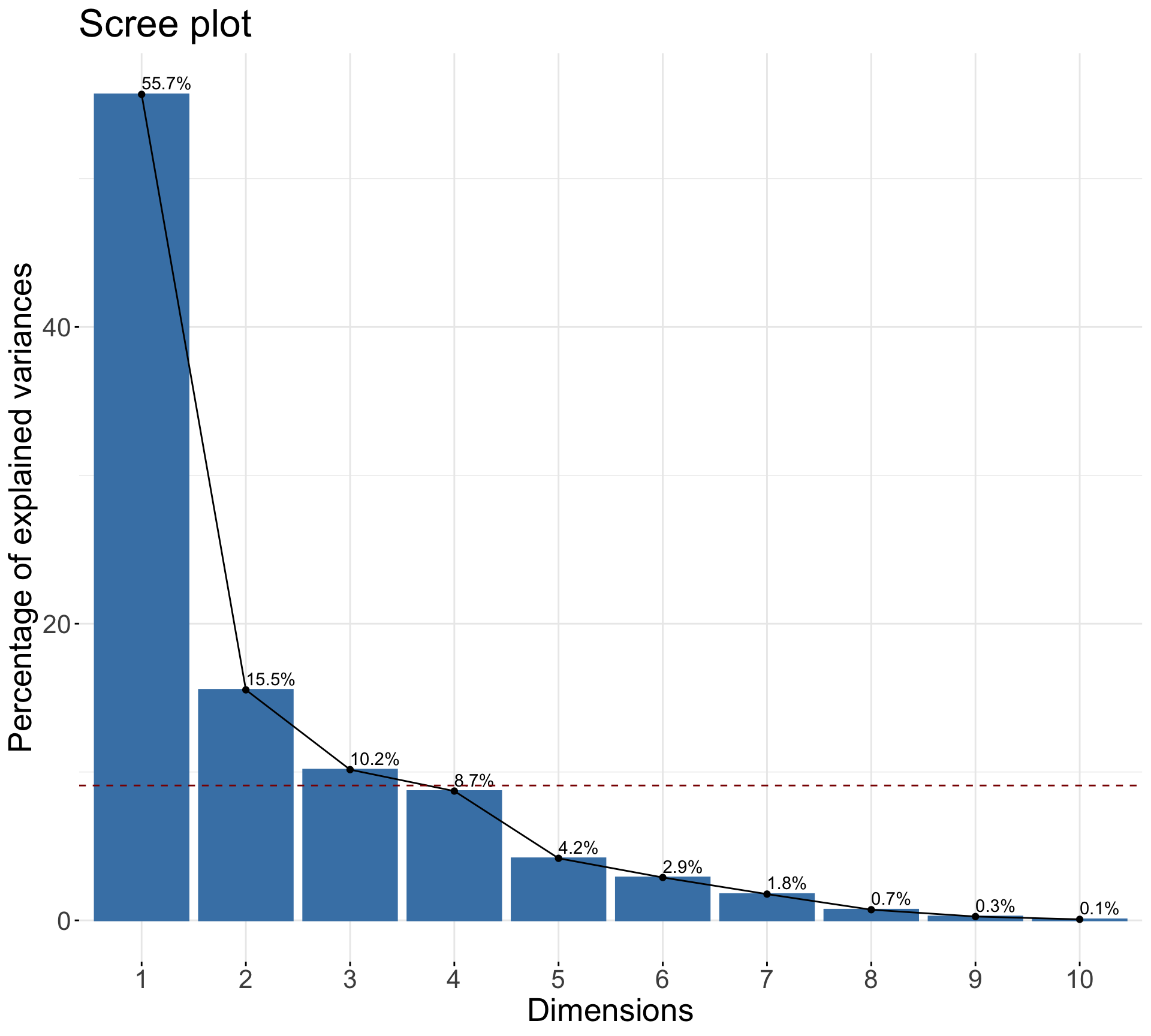
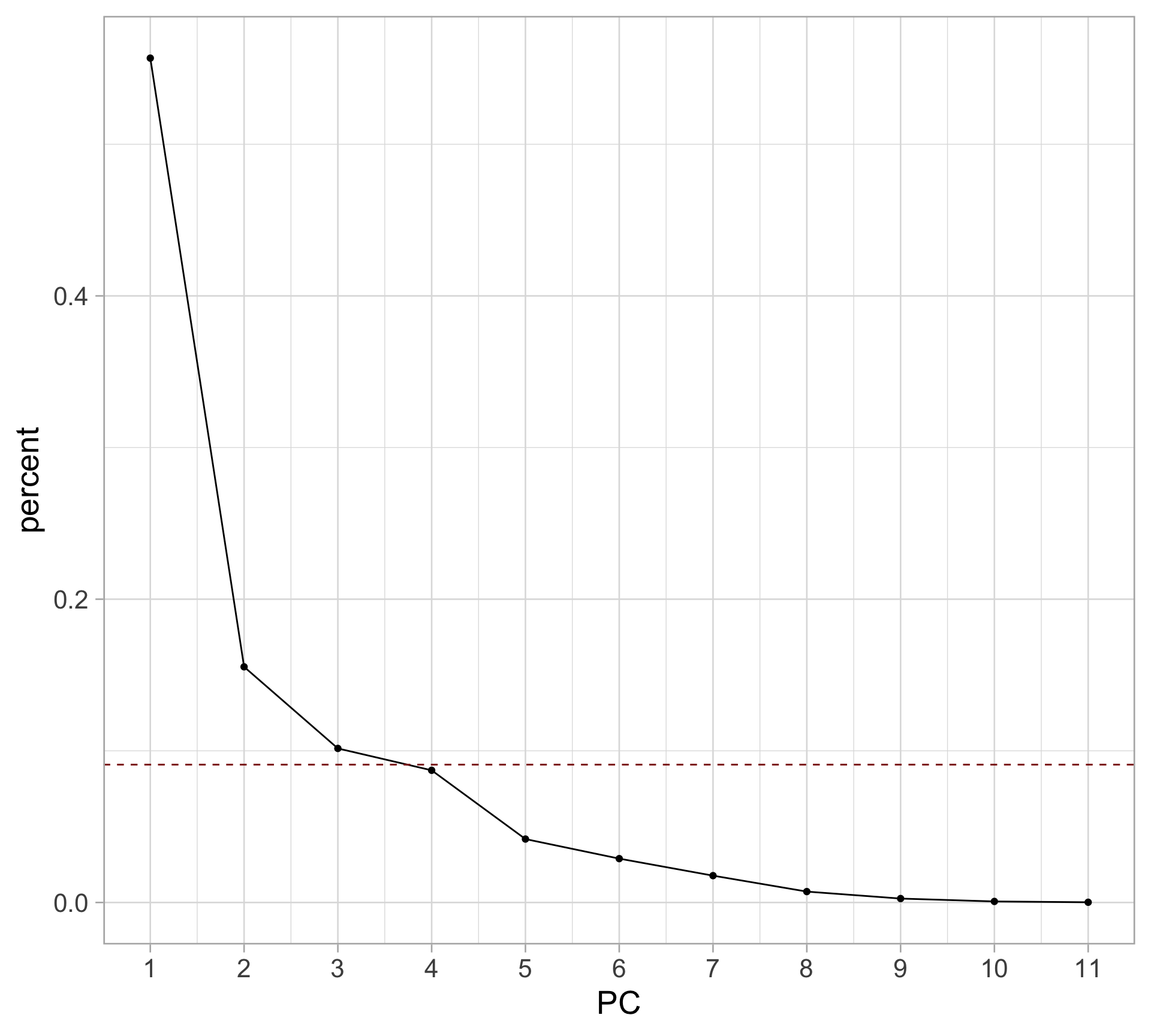
Rows: 1,147
Columns: 15
$ product_name <chr> "brewed coffee - dark roast", "brewed coffee - dark ro…
$ size <chr> "short", "tall", "grande", "venti", "short", "tall", "…
$ milk <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, …
$ whip <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ serv_size_m_l <dbl> 236, 354, 473, 591, 236, 354, 473, 591, 236, 354, 473,…
$ calories <dbl> 3, 4, 5, 5, 3, 4, 5, 5, 3, 4, 5, 5, 3, 4, 5, 5, 35, 50…
$ total_fat_g <dbl> 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1,…
$ saturated_fat_g <dbl> 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,…
$ trans_fat_g <dbl> 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,…
$ cholesterol_mg <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10,…
$ sodium_mg <dbl> 5, 10, 10, 10, 5, 10, 10, 10, 5, 5, 5, 5, 5, 5, 5, 5, …
$ total_carbs_g <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 5, …
$ fiber_g <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ sugar_g <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 5, …
$ caffeine_mg <dbl> 130, 193, 260, 340, 15, 20, 25, 30, 155, 235, 310, 410…