Supervised learning: linear regression
SURE 2025
Department of Statistics & Data Science
Carnegie Mellon University
Background
Supervised learning
- General setup: Given a dataset of \(n\) observations (rows) and \(p\) variables (columns)
- Response/outcome/target/dependent variable \(Y\) in one of the \(p\) variables
Goal: uncover associations between a set of predictors/features/covariates/explanatory variables and a response variable
Accurately predict unseen test cases
Understand which features affect the response (and how)
Assess the quality of our predictions and inferences
Two main types of problems
Regression: estimate average value of response (i.e. the response is quantitative)
Classification: determine the most likely class of a set of discrete response variable classes (i.e. the response is categorical)
Examples of supervised learning methods
Linear regression (today)
Generalized linear models (GLMs) and penalized versions (lasso, ridge, elastic net)
Smoothing splines, generalized additive models (GAMs)
Decision trees and its variants (e.g., random forests, boosting)
Deep learning, neural networks
Resources
Advanced Data Analysis from an Elementary Point of View (aka the greatest book that will never be published)
“Regression”, in statistical jargon, is the problem of guessing the average level of some quantitative response variable from various predictor variables. - Note GOAT
Simple linear regression
Linear regression is used when the response variable is quantitative
Assume a linear relationship for \(Y = f(X)\) \[Y_{i}=\beta_{0}+\beta_{1} X_{i}+\epsilon_{i}, \quad \text { for } i=1,2, \dots, n\]
\(Y_i\) is the \(i\)th value for the response variable
\(X_i\) is the \(i\)th value for the predictor variable
\(\beta_0\) is an unknown, constant intercept
- average value for \(Y\) if \(X = 0\) (be careful sometimes…)
\(\beta_1\) is an unknown, constant slope
- change in average value for \(Y\) for each one-unit increase in \(X\)
\(\epsilon_i\) is the random noise
assume independent, identically distributed (iid) from a normal distribution
\(\epsilon_i \overset{iid}{\sim}N(0, \sigma^2)\) with constant variance \(\sigma^2\)
Simple linear regression estimation
We are estimating the conditional expection (mean) for \(Y\):
\[\mathbb{E}[Y_i \mid X_i] = \beta_0 + \beta_1X_i\]
- average value for \(Y\) given the value for \(X\)
How do we estimate the best fitted line?
Ordinary least squares (OLS) - by minimizing the residual sum of squares (RSS)
\[\text{RSS} \left(\beta_{0}, \beta_{1}\right)=\sum_{i=1}^{n}\left[Y_{i}-\left(\beta_{0}+\beta_{1} X_{i}\right)\right]^{2}=\sum_{i=1}^{n}\left(Y_{i}-\beta_{0}-\beta_{1} X_{i}\right)^{2}\]
\[\widehat{\beta}_{1}=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \quad \text{ and } \quad \widehat{\beta}_{0}=\bar{Y}-\widehat{\beta}_{1} \bar{X}\]
where \(\displaystyle \bar{X} = \frac{1}{n}\sum_{i=1}^n X_i\) and \(\displaystyle \bar{Y} = \frac{1}{n}\sum_{i=1}^n Y_i\)
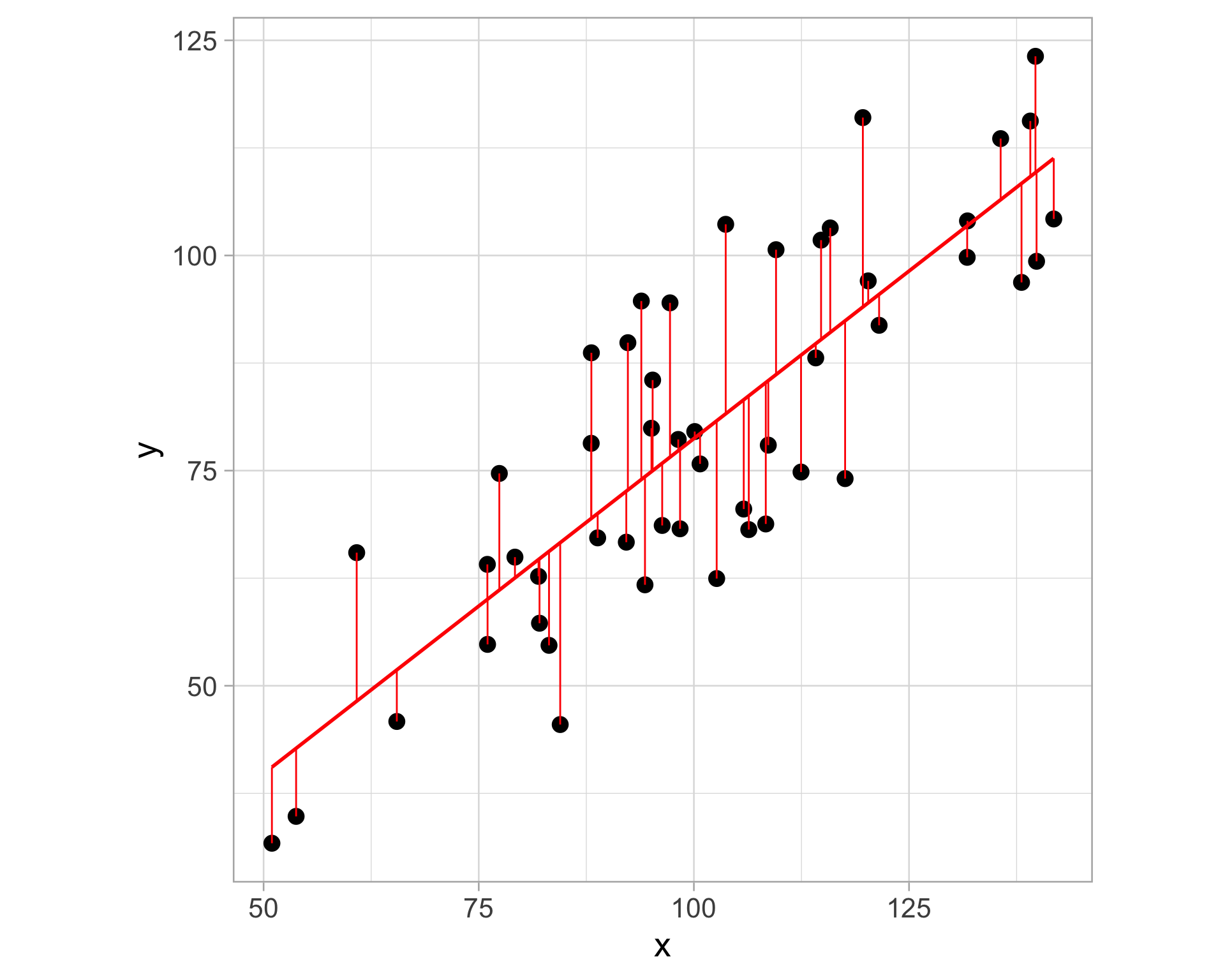
Visual explanation
Imagine a 2D scatterplot with different data points
Linear regression aims to find a “best fit” line that minimizes the vertical distance between the line and the data points
- The vertical distance is known as a residual (difference between the actual y-value of a data point and the predicted y-value on the regression line)
Linear regression in R
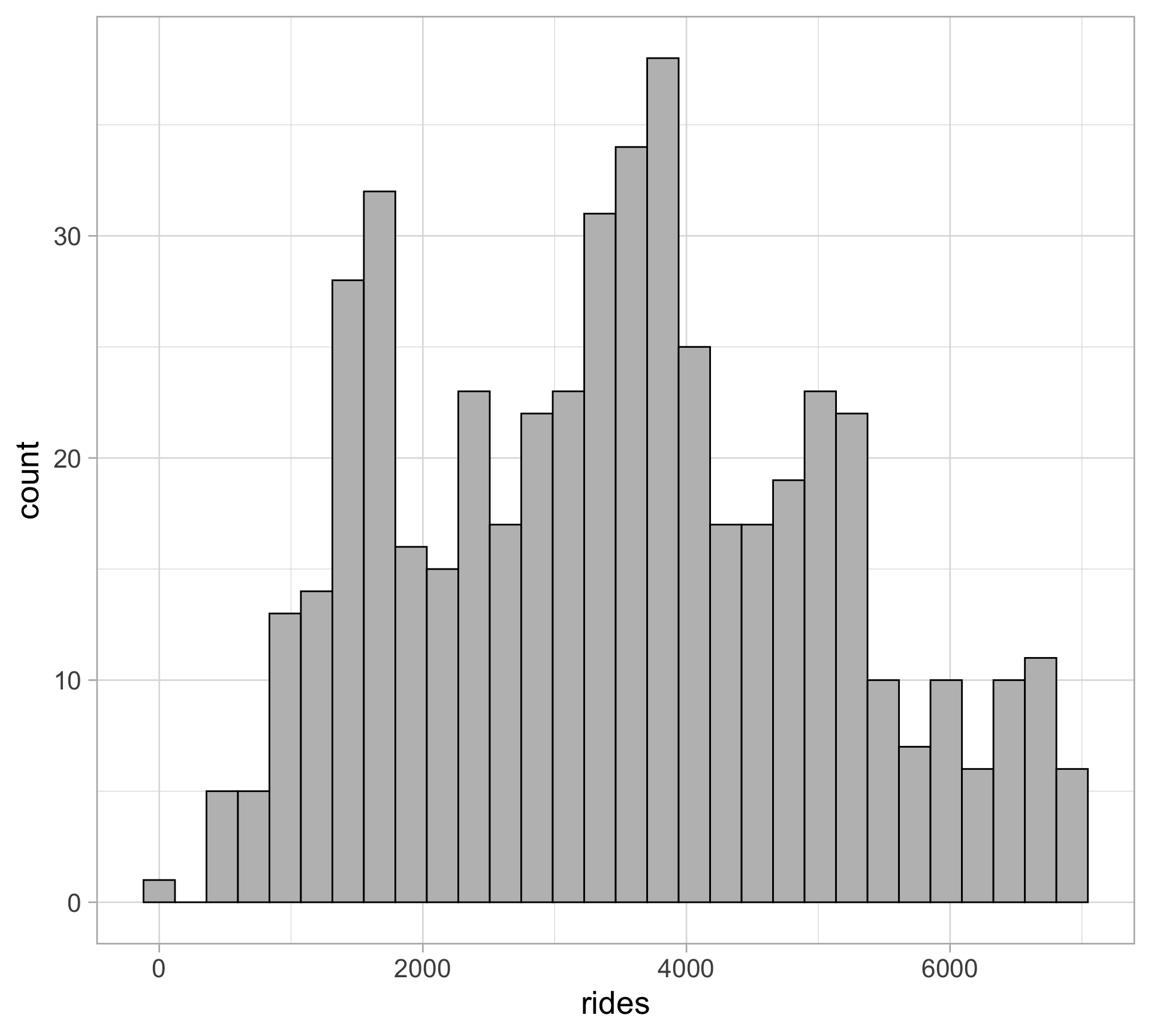
Data: Capital Bikeshare Ridership
Daily count of rental bikes between years 2011 and 2012 in Capital bikeshare system with the corresponding weather and seasonal information.
library(tidyverse)
theme_set(theme_light())
bikes <- read_csv("https://raw.githubusercontent.com/36-SURE/2025/refs/heads/main/data/bikes.csv")
glimpse(bikes)Rows: 500
Columns: 13
$ date <date> 2011-01-01, 2011-01-03, 2011-01-04, 2011-01-05, 2011-01-0…
$ season <chr> "winter", "winter", "winter", "winter", "winter", "winter"…
$ year <dbl> 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011…
$ month <chr> "Jan", "Jan", "Jan", "Jan", "Jan", "Jan", "Jan", "Jan", "J…
$ day_of_week <chr> "Sat", "Mon", "Tue", "Wed", "Fri", "Sat", "Mon", "Tue", "W…
$ weekend <lgl> TRUE, FALSE, FALSE, FALSE, FALSE, TRUE, FALSE, FALSE, FALS…
$ holiday <chr> "no", "no", "no", "no", "no", "no", "no", "no", "no", "no"…
$ temp_actual <dbl> 57.39952, 46.49166, 46.76000, 48.74943, 46.50332, 44.17700…
$ temp_feel <dbl> 64.72625, 49.04645, 51.09098, 52.63430, 50.79551, 46.60286…
$ humidity <dbl> 80.5833, 43.7273, 59.0435, 43.6957, 49.8696, 53.5833, 48.2…
$ windspeed <dbl> 10.749882, 16.636703, 10.739832, 12.522300, 11.304642, 17.…
$ weather_cat <chr> "categ2", "categ1", "categ1", "categ1", "categ2", "categ2"…
$ rides <dbl> 654, 1229, 1454, 1518, 1362, 891, 1280, 1220, 1137, 1368, …Modeling bike ridership
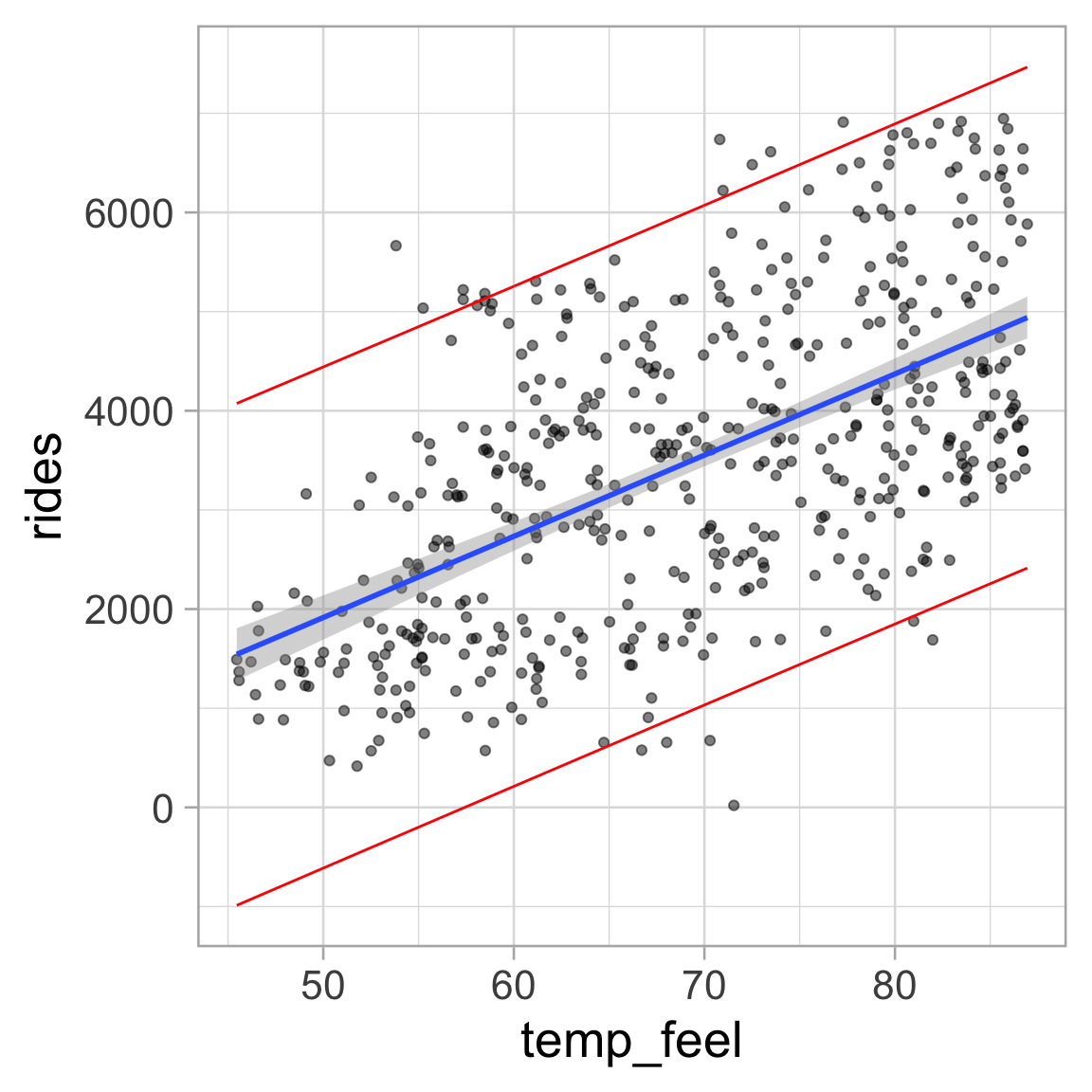
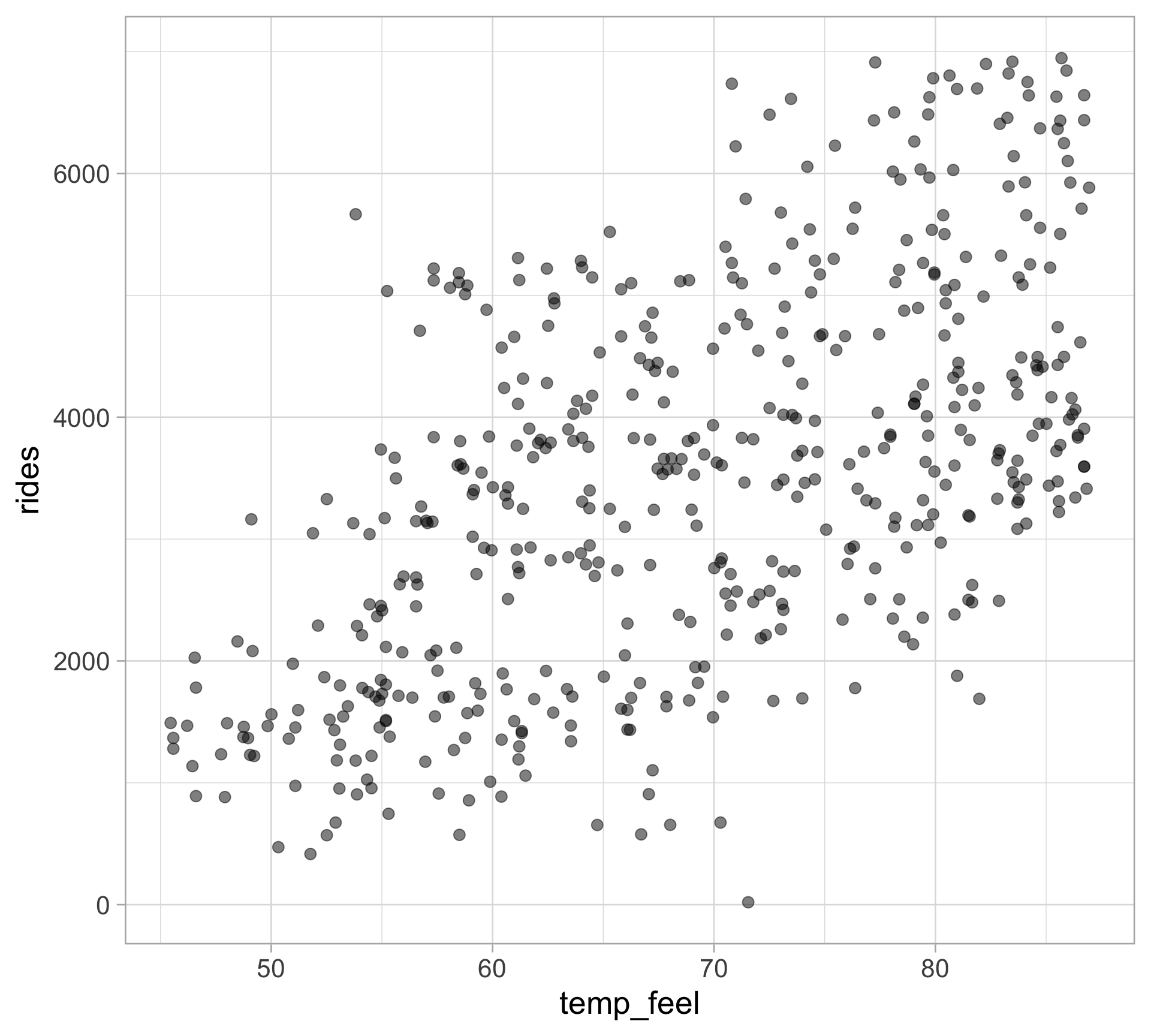
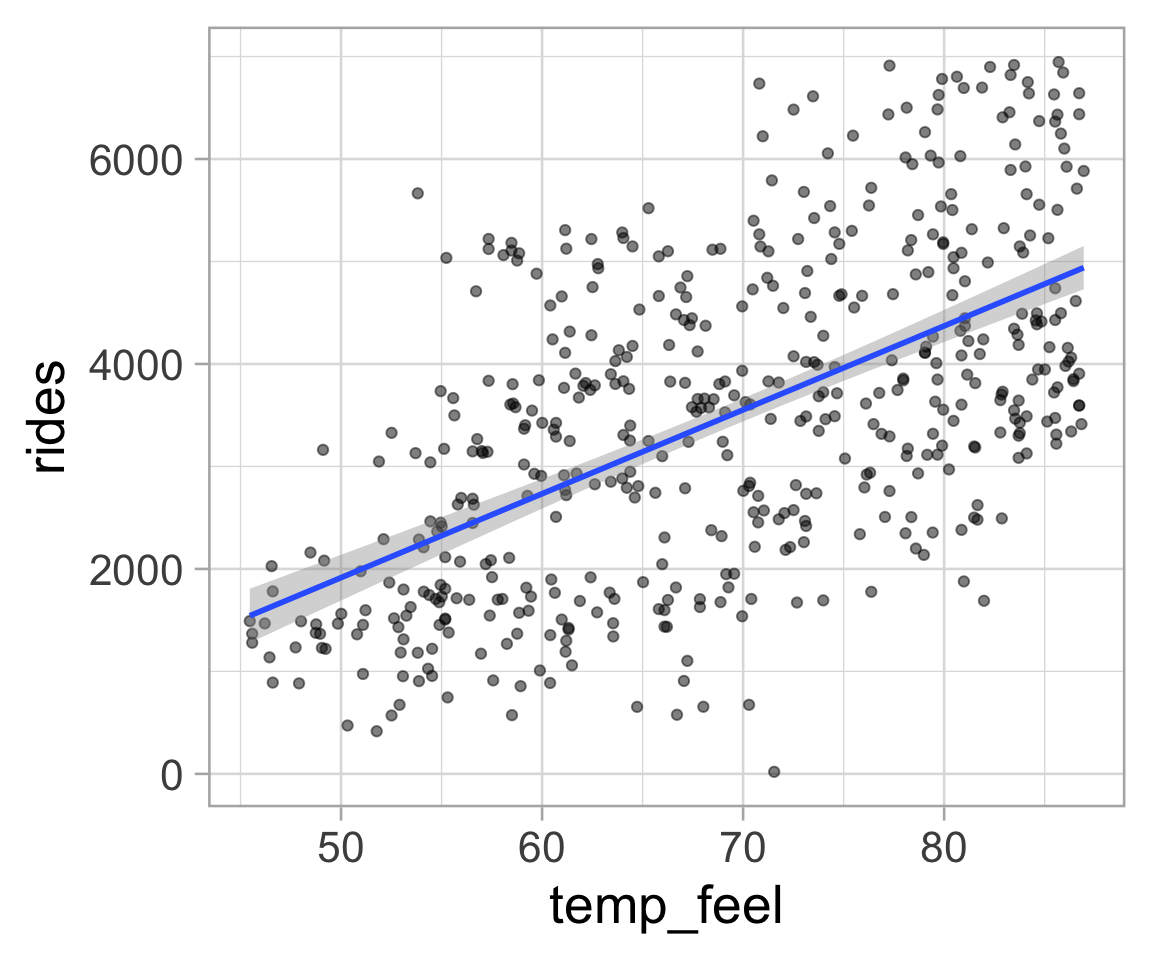
Relationship between rides and feels-like temperature
Model summary using summary()
Call:
lm(formula = rides ~ temp_feel, data = bikes)
Residuals:
Min 1Q Median 3Q Max
-3658.9 -1029.7 -149.7 950.6 3437.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2179.27 358.63 -6.077 2.44e-09 ***
temp_feel 81.88 5.12 15.992 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1281 on 498 degrees of freedom
Multiple R-squared: 0.3393, Adjusted R-squared: 0.338
F-statistic: 255.7 on 1 and 498 DF, p-value: < 2.2e-16How do we read the summary output?
Model: \(\ \small \text{Rides} = \beta_0 + \beta_1 \ \text{Temperature} + \epsilon\)
From output: \(\ \small \hat{\beta}_0 = -2179.27\) and \(\small \hat{\beta}_1 = 81.88\)
OLS line: \(\ \ \small \widehat{\text{Rides}} = -2179.27 + 81.88 \ \text{Temperature}\)
Interpretation of \(\hat \beta_1\): estimated change in y for a one unit change in x
In context: For every additional \(^{\circ}\) F in feels-like temperature, the expected ridership increases by about 82 rides.
Inference: hypothesis testing
Call:
lm(formula = rides ~ temp_feel, data = bikes)
Residuals:
Min 1Q Median 3Q Max
-3658.9 -1029.7 -149.7 950.6 3437.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2179.27 358.63 -6.077 2.44e-09 ***
temp_feel 81.88 5.12 15.992 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1281 on 498 degrees of freedom
Multiple R-squared: 0.3393, Adjusted R-squared: 0.338
F-statistic: 255.7 on 1 and 498 DF, p-value: < 2.2e-16Estimates of uncertainty for model coefficients via standard errors \[\quad \widehat{SE}(\hat{\beta}_0) = 358.63 \quad \text{and} \quad \widehat{SE}(\hat{\beta}_1) = 5.12\]
We’re testing whether there is a linear relationship between the predictor and the response \[\quad H_0: \beta_1 = 0 \quad \text{vs} \quad H_1: \beta_1 \neq 0\]
Test statistic: \[t = \frac{\hat{\beta}_1}{\widehat{SE}(\hat{\beta}_1)} = \frac{81.88}{5.12} = 15.99\]
Inference: hypothesis testing
Call:
lm(formula = rides ~ temp_feel, data = bikes)
Residuals:
Min 1Q Median 3Q Max
-3658.9 -1029.7 -149.7 950.6 3437.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2179.27 358.63 -6.077 2.44e-09 ***
temp_feel 81.88 5.12 15.992 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1281 on 498 degrees of freedom
Multiple R-squared: 0.3393, Adjusted R-squared: 0.338
F-statistic: 255.7 on 1 and 498 DF, p-value: < 2.2e-16Recall that we’re testing \[\quad H_0: \beta_1 = 0 \quad \text{vs} \quad H_1: \beta_1 \neq 0\]
\(p\)-value (i.e.,
Pr(>|t|)): probability of observing a value as extreme as the observed test statistic (under the null hypothesis)\(p\)-value \(< \alpha = 0.05\) (conventional threshold): sufficient evidence to reject the null hypothesis that the coefficient is zero
In context: There is a statistically significant association between temperature and number of bikeshare rides, \(\small \hat \beta_1 = 81.88, t = 15.99,p\)-value \(<0.001\).
Model summary using the broom package
The 3 broom functions (Note: the output is always a tibble)
tidy(): coefficients table in a tidy formatglance(): produces summary metrics of a model fitaugment(): adds/“augments” columns to the original data (e.g., adding predictions)
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -2179. 359. -6.08 2.44e- 9
2 temp_feel 81.9 5.12 16.0 9.29e-47# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.339 0.338 1281. 256. 9.29e-47 1 -4286. 8579. 8591.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Confidence interval for model coefficients
# A tibble: 2 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -2179. 359. -6.08 2.44e- 9 -2884. -1475.
2 temp_feel 81.9 5.12 16.0 9.29e-47 71.8 91.9In-context interpretation (for temp_feel)
- For every additional \(^{\circ}\) F in feels-like temperature, the expected ridership increases by about 82 rides (95% CI [71.8, 91.9])
- We’re 95% confident that every additional degree Fahrenheit in temperature is associated with an increase of about 72 to 92 rides in expected ridership.
Coefficient of determination
- In linear regression, the square of the correlation coefficient happens to be exactly the coefficient of determination
\(R^2\) estimates the proportion of the variance of \(Y\) explained by \(X\)
More generally: variance of model predictions / variance of \(Y\)
- Interpretation: 33.9% of the variability in the number of bikeshare rides can be explained by the linear relationship between ridership and feels-like temperature (the remaining 66.1% of the variation is due to other factors and/or noise)
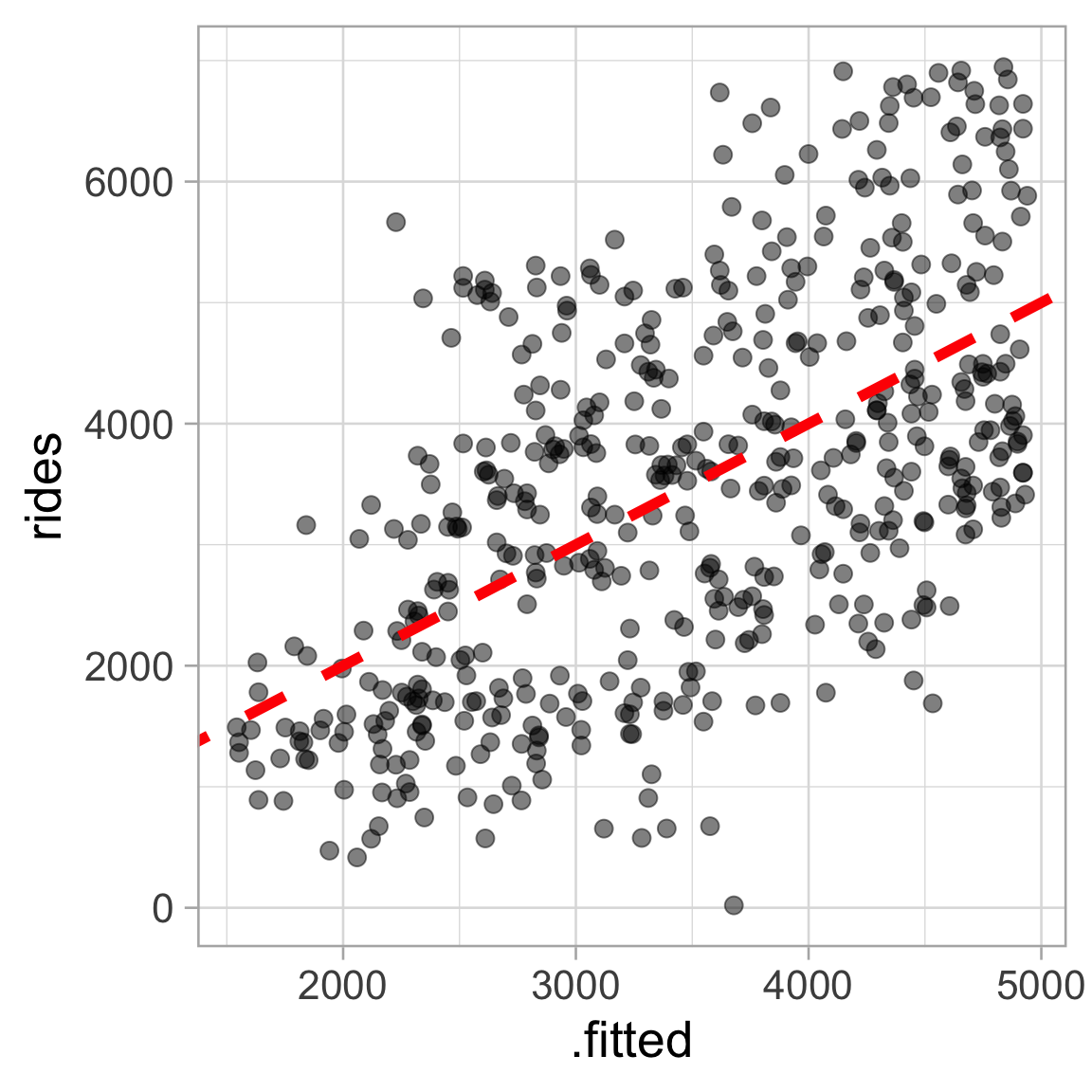
Generating predictions
We can use the predict() or fitted() function to get the fitted values from the regression model
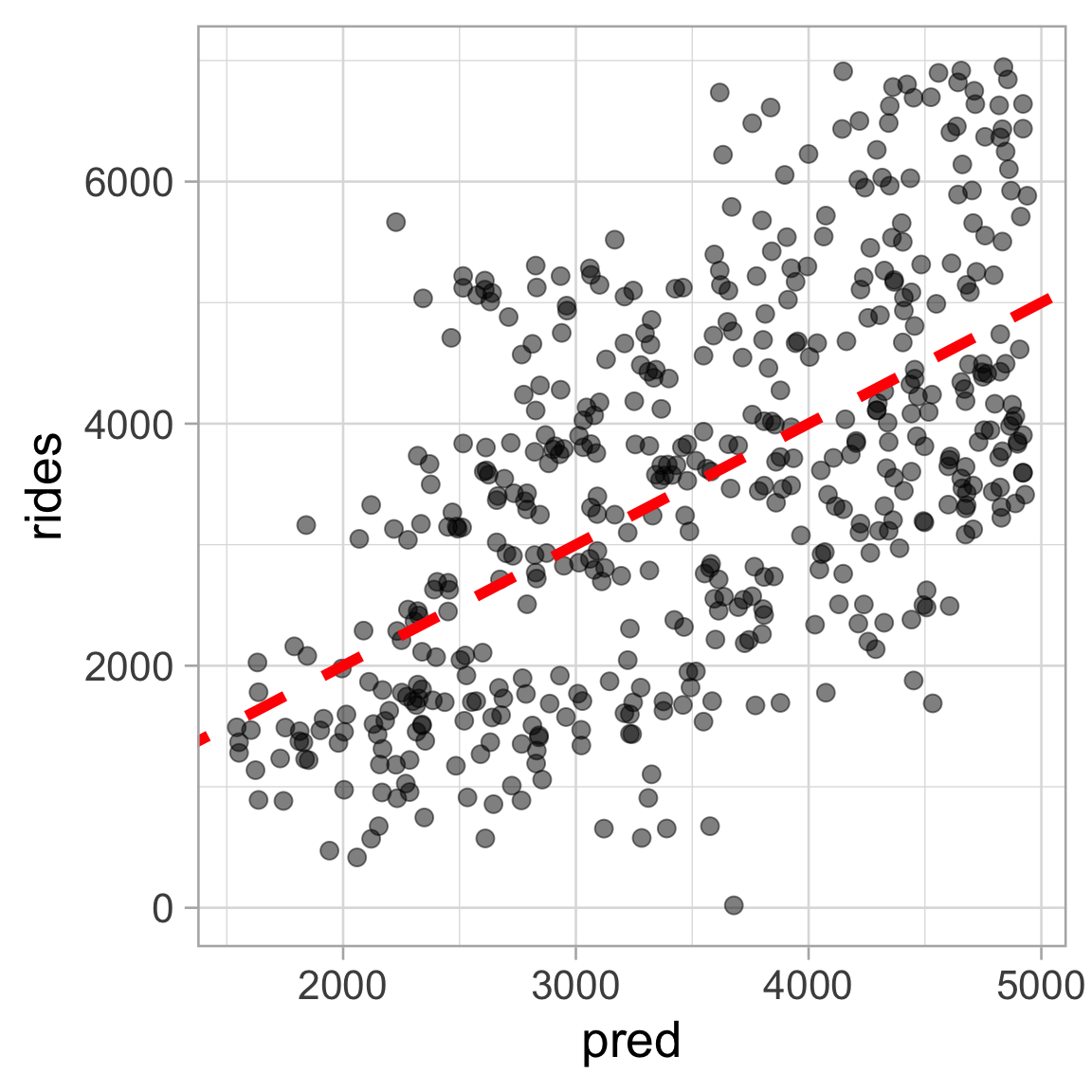
Plot observed values against predictions
Useful diagnostic (for any type of model, not just linear regression!)
Plot observed values against predictions
Augment the data with model output using the broom package
augment() adds various columns from model fit we can use in plotting for model diagnostics
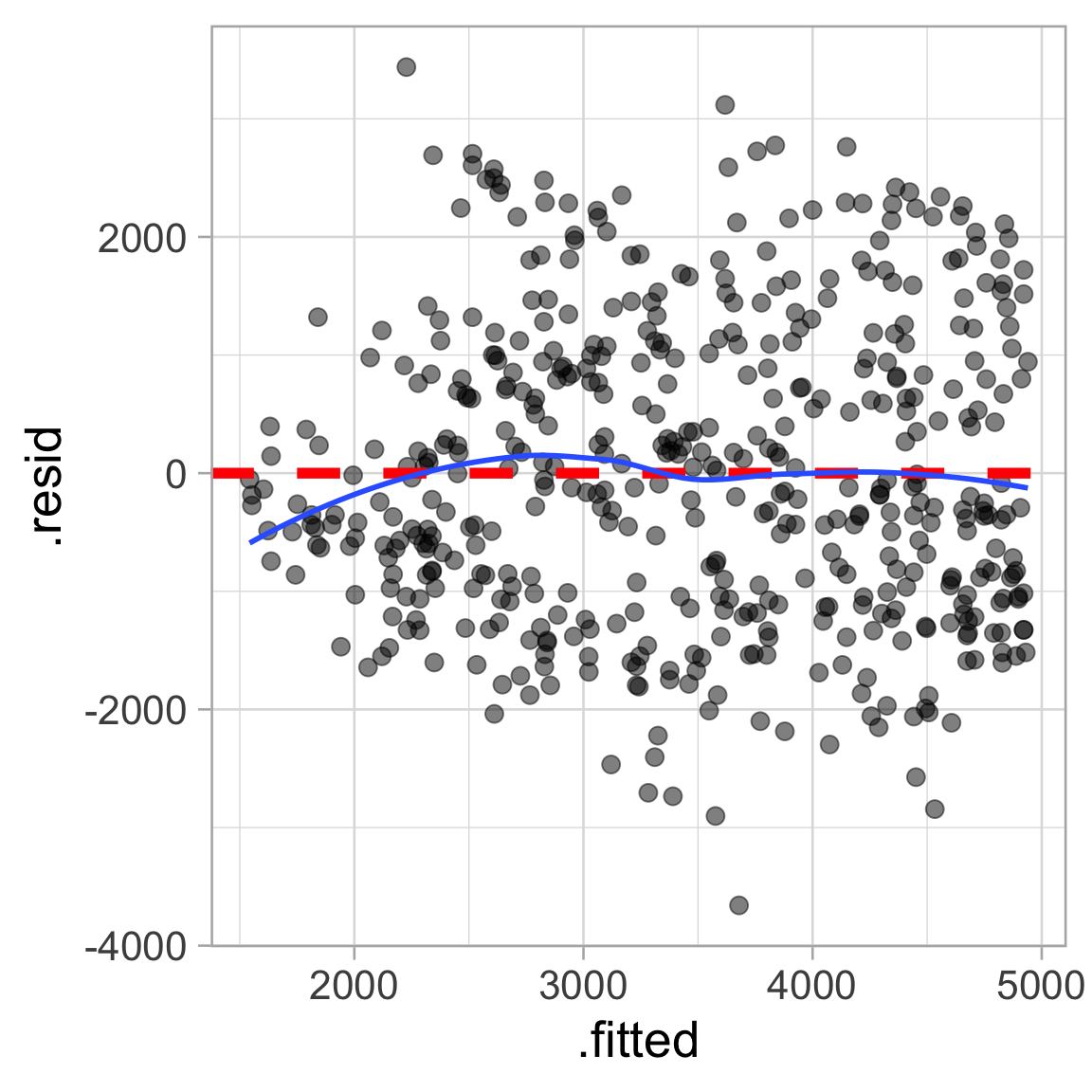
Assessing assumptions of linear regression
Simple linear regression assumes \(Y_i \overset{iid}{\sim} N(\beta_0 + \beta_1 X_i, \sigma^2)\)
- If this is true, then \(Y_i - \hat{Y}_i \overset{iid}{\sim} N(0, \sigma^2)\)
Plot residuals against \(\hat{Y}_i\), residuals vs fit plot
Used to assess linearity, any divergence from mean 0
Used to assess equal variance, i.e., if \(\sigma^2\) is homogenous across predictions/fits \(\hat{Y}_i\)
More difficult to assess the independence and fixed \(X\) assumptions
- Make these assumptions based on subject-matter knowledge
Plot residuals against predicted values
Residuals = observed - predicted
Interpretation of residuals in context?
Conditional on the predicted values, the residuals should have a mean of zero
Residuals should NOT display any pattern
Two things to look for:
Any trend around horizontal reference line?
Equal vertical spread?
Linear regression with one categorical predictor
- Model
ridesby theseason(4 levels:spring,summer,fall,winter)
We are changing the intercept of our regression line by including a categorical variable
Notice we only get 3 coefficients for the season besides the intercept \[\widehat{\text{Rides}} = 4051 - 265 \ I_{\texttt{spring}} + 543 \ I_{\texttt{summer}} - 1686 \ I_{\texttt{winter}}\]
# A tibble: 4 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 4051. 107. 38.0 7.15e-149 3841. 4260.
2 seasonspring -265. 158. -1.68 9.35e- 2 -574. 44.8
3 seasonsummer 543. 246. 2.21 2.76e- 2 60.2 1027.
4 seasonwinter -1686. 152. -11.1 1.11e- 25 -1985. -1388. Linear regression with one categorical predictor
\[\widehat{\text{Rides}} = 4050.7 - 264.7 \ I_{\texttt{spring}} + 543.5 \ I_{\texttt{summer}} - 1686.3 \ I_{\texttt{winter}}\]
By default,
Rturns the categorical variables of \(m\) levels (e.g. 4 seasons in this dataset) into \(m-1\) indicator/dummy variables for different categories relative to a baseline/reference levelIndicator/dummy variables: binary variables (1: that level, 0: not that level)
Ruses alphabetical order to determine the reference level (fallseason in this case)
Linear regression with one categorical predictor
\[\widehat{\text{Rides}} = 4050.7 - 264.7 \ I_{\texttt{spring}} + 543.5 \ I_{\texttt{summer}} - 1686.3 \ I_{\texttt{winter}}\]
The intercept term gives us the (baseline) average y for the reference level
- In context, the expected daily bikeshare rides during fall season is 4051 rides (95% CI [3841, 4260])
The values for the coefficient estimates indicate the expected change in the response variable relative to the reference level
- For example, the expected bikeshare rides during winter is 1686 rides lower (95% CI [-1985, -1388]) than during fall (does this make sense?)
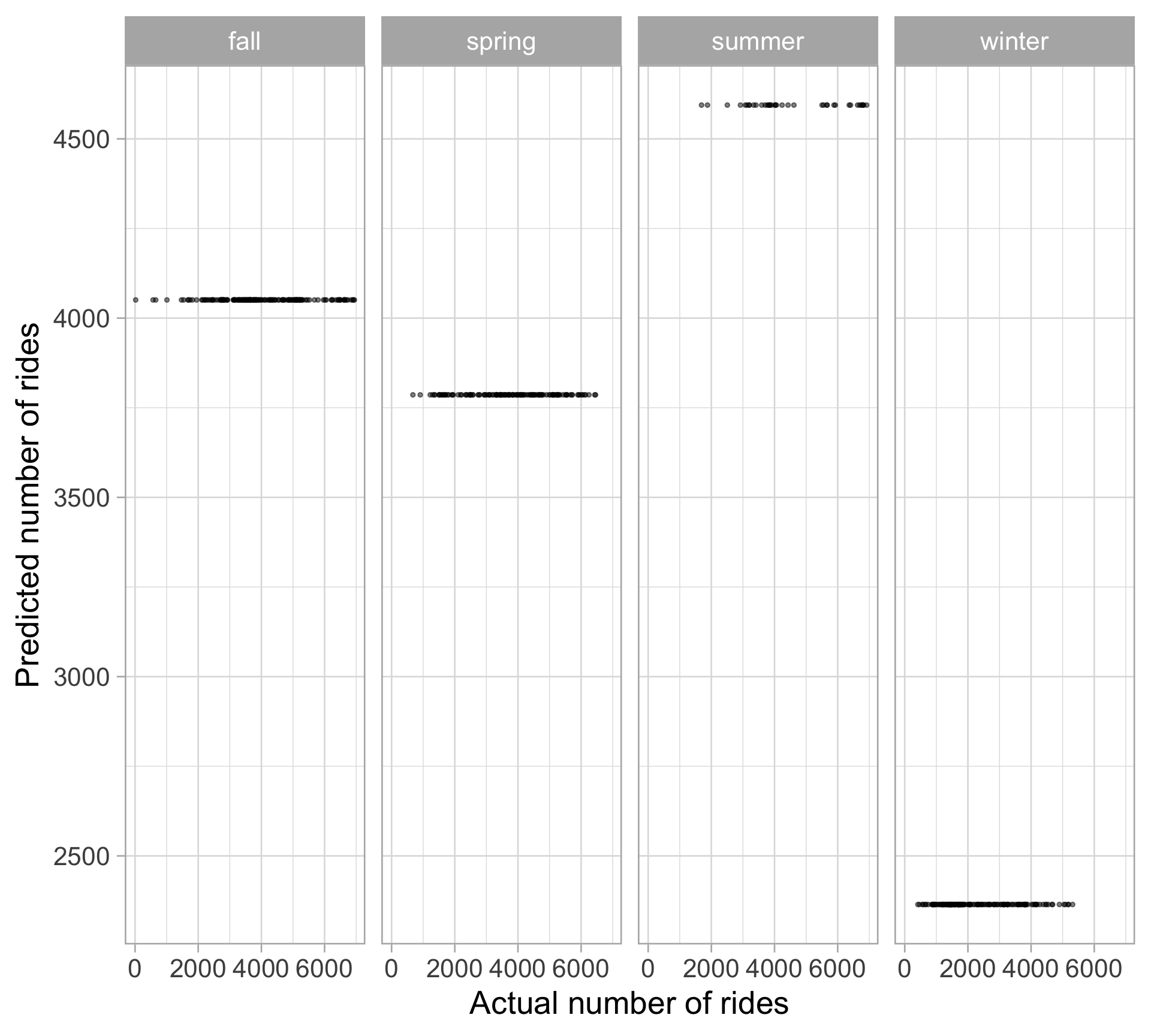
Comparing observed values and predictions
Similar to before, we can plot the actual and predicted ridership
To reiterate, all we’re doing is changing the intercept of our regression line by including a categorical variable
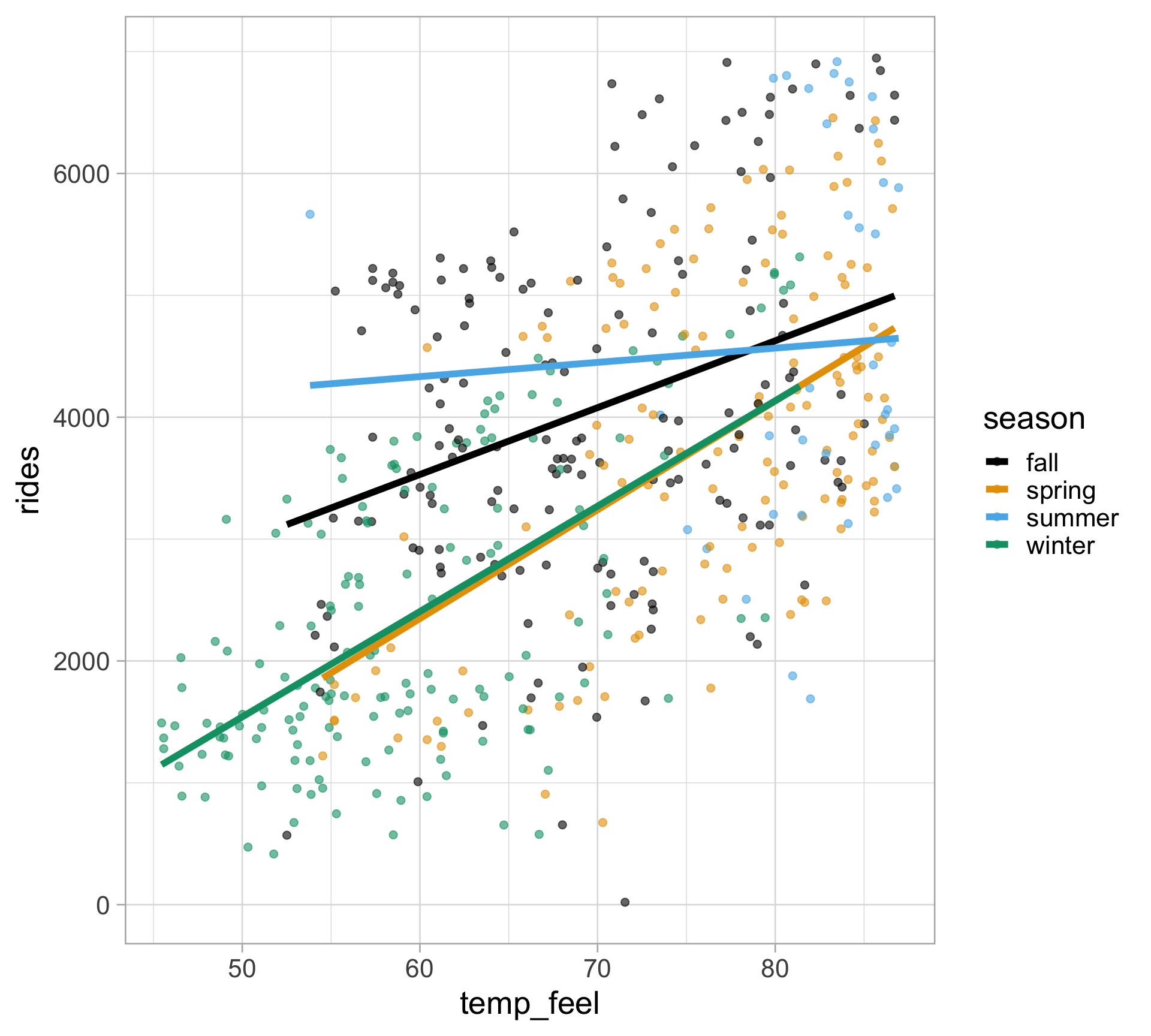
Interactions
- An interaction allows one predictor’s association with the outcome to depend on values of another predictor
Example: interaction between a categorical variable (
season) and a quantitative variable (temp_feel)When to include interaction? When we believe relationships between a quantitative variable and the response differ across categories (of a categorical variable)
4 different lines for each
seasonin modeling relationship betweenridesandtemp_feelThis means those regression lines have different intercepts as well as different slopes
- For more on interactions, see these notes
Visualizing interactions
Interpreting interactions
\[ \begin{aligned} {\text{Rides}} &= \beta_0 + \beta_1 \ \text{Temp} + \beta_2 \ I_{\texttt{spring}} + \beta_3 \ I_{\texttt{summer}} + \beta_4 \ I_{\texttt{winter}} \\ &+ \beta_5 \{ \text{Temp } \times I_{\texttt{spring}} \} + \beta_6 \{ \text{Temp } \times I_{\texttt{summer}} \} + \beta_7 \{ \text{Temp } \times I_{\texttt{winter}} \} + \epsilon \\ \end{aligned} \]
# A tibble: 8 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 238. 773. 0.308 0.758
2 temp_feel 54.9 11.0 4.97 0.000000935
3 seasonspring -3244. 1222. -2.65 0.00819
4 seasonsummer 3393. 2921. 1.16 0.246
5 seasonwinter -3020. 1032. -2.93 0.00358
6 temp_feel:seasonspring 34.4 16.6 2.07 0.0386
7 temp_feel:seasonsummer -43.2 35.9 -1.20 0.229
8 temp_feel:seasonwinter 31.6 15.8 1.99 0.0466 \(\beta_0\) and \(\beta_1\) give the slope and intercept for the regression line (describing the relationship between ridership & temperature) for fall season (the reference level)
\(\beta_2\) measures the difference in the intercepts between spring and fall seasons
\(\beta_5\) shows how much the slopes change as we move from the regression line for fall (the reference level) to the line for spring
and so on…
Multiple linear regression
We can include as many variables as we want (assuming \(n > p\))
\[Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{p} X_{p}+\epsilon\]
OLS estimates in matrix notation (\(\boldsymbol{X}\) is a \(n \times p\) matrix):
\[\hat{\boldsymbol{\beta}} = (\boldsymbol{X} ^T \boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{Y}\]
Can just add more variables to the formula in R
Use adjusted \(R^2\) when including multiple variables \(\displaystyle 1 - \frac{(1 - R^2)(n - 1)}{(n - p - 1)}\)
Adjusts for the number of variables in the model \(p\)
Adding more variables will always increase the model’s (unadjusted) \(R^2\)
READ THIS: \(R^2\) myths
What about the normality assumption?
Model: \(Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{p} X_{p}+\epsilon\)
\(\epsilon_i\) is the random noise: assume independent and identically distributed (iid) from a Normal distribution \(\epsilon_i \overset{iid}{\sim}N(0, \sigma^2)\) with constant variance \(\sigma^2\)
- OLS doesn’t care about this assumption, it’s just estimating coefficients!
In order to perform inference, we need to impose additional assumptions
By assuming \(\epsilon_i \overset{iid}{\sim}N(0, \sigma^2)\), what we really mean is \(Y \overset{iid}{\sim}N(\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{p} X_{p}, \sigma^2)\)
- So we’re estimating the mean \(\mu\) of this conditional distribution, but what about \(\sigma^2\)?
Unbiased estimate \(\displaystyle \hat{\sigma}^2 = \frac{\text{RSS}}{n - (p + 1)}\)
Degrees of freedom: \(n - (p + 1)\), data supplies us with \(n\) “degrees of freedom” and we used up \(p + 1\)
Regression confidence intervals vs prediction intervals
Do we want to predict the mean response for a particular value \(x^*\) of the explanatory variable or do we want to predict the response for an individual case?
Example:
if we would like to know the average ridership for all days with feels-like temperature of 70 degrees Fahrenheit, then we would use an interval for the mean response
if we want an interval to contain the ridership of a particular day with feels-like temperature of 70 degrees Fahrenheit, then we need the interval for a single prediction
Regression confidence intervals
Regression confidence intervals
Interval estimate for the MEAN response at a given observation (i.e. for the predicted AVERAGE \(\hat{\beta}_0 + \hat{\beta}_1 x^*\))
Based on standard errors for the estimated regression line at \(x^*\) \[SE_{\text{line}}\left(x^{*}\right)=\hat{\sigma} \cdot \sqrt{\frac{1}{n}+\frac{\left(x^{*}-\bar{x}\right)^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}}\]
Variation only comes from uncertainty in the parameter
Regression prediction intervals
interval estimate for an INDIVIDUAL response at a given (new) observation
add the variance \(\sigma^2\) of a single predicted value \[SE_{\text{pred}}\left(x^{*}\right)=\hat{\sigma} \cdot \sqrt{1 + \frac{1}{n}+\frac{\left(x^{*}-\bar{x}\right)^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}}\]
Variation comes from uncertainty in parameter estimates and error variance
Confidence intervals versus prediction intervals
Generate 95% intervals
The standard error for predicting an individual response will always be larger than for predicting a mean response
Prediction intervals will always be wider than confidence intervals