Supervised learning: regularization

SURE 2025

Department of Statistics & Data Science
Carnegie Mellon University

Background

Shortcomings of linear regression

• Predictability

  • Recall that we can decompose estimation (prediction) error into squared bias and variance

  • Linear regression: high bias, low variance

• Variable selection

  • With a large number of predictors, it can be helpful to identify a subset of relevant features and eliminate uninformative ones

  • Linear regression “freely” assigns a coefficient to each predictor variable

  • Can we have a model fitting procedure that make only a subset of the coefficients large, and others small (or even better, zero)?

The big picture

Regularized/shrinkage/penalized regression

• Involves fitting a model containing all \(p\) predictors

• However, the estimated coefficients are shrunken towards zero relative to the least squares estimates of vanilla linear regression

• This “shrinkage” (also known as regularization) has the effect of reducing variance

• Depending on what type of regularization is performed, some coefficient estimates can be exactly zero

• Thus, regularization methods (e.g. LASSO) can perform variable selection

Recap: linear regression

• Linear regression (least squares) estimates coefficients by minimizing

\[\text{RSS} = \sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2\]

Ridge regression

Linear regression vs ridge regression

• Linear regression (least squares) estimates coefficients by minimizing

\[\text{RSS} = \sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2\]

• Ridge regression introduces a shrinkage penalty term and minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p \beta_j^2 = \text{RSS} + \lambda \sum_{j=1}^p \beta_j^2\]

• Ridge regression uses a (squared) \(\ell_2\) penalty (hence ridge is also known as \(\ell_2\) regularization)

  • The \(\ell_2\) norm of a coefficient vector \(\beta\) is given by \(\displaystyle \Vert \beta \Vert_2 = \sqrt{\sum_{j=1}^p \vert \beta_j \vert ^2}\)

Ridge regression: more details

• Recall that ridge regression minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p \beta_j^2 = \text{RSS} + \lambda \sum_{j=1}^p \beta_j^2\]

• Here, \(\lambda \ge 0\) is a tuning parameter, which controls the strength of the penalty term

• Use cross-validation to tune \(\lambda\) (for a fixed value of \(\lambda\), ridge regression fits only a single model)

• As \(\lambda\) increases, flexibility of models decreases (bias increases, variance decreases)

  • When \(\lambda = 0\), it’s just linear regression

  • When \(\lambda \rightarrow \infty\), the coefficient estimates approach 0

  • For \(\lambda\) in between, we are balancing two ideas: fitting a linear model and shrinking the coefficients

Ridge regression: textbook example

• Notice how the magnitude of the coefficients for the 4 highlighted variables trend as \(\lambda \rightarrow \infty\)

• The coefficients shrink towards zero, but never actually reach it

Lasso & sparsity

Moving from ridge to lasso

• Ridge never sets coefficients to exactly zero (i.e., always keeps all variables)

• Therefore ridge regression cannot perform variable selection

• But we may believe there is a sparse solution (i.e., a model involving only a subset of the variables)

• Entering the lasso (least absolute shrinkage and selection operator)

• Compared to ridge, one big advantage of lasso/sparsity: it performs variable selection in the linear model, so we can understand which relevant features the model relies on for prediction

Linear regression vs ridge vs lasso

• Linear regression (least squares) estimates coefficients by minimizing

\[\text{RSS} = \sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2\]

• Ridge regression minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p \beta_j^2 = \text{RSS} + \lambda \sum_{j=1}^p \beta_j^2\]

• Lasso regression enables variable selection by minimizing

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p\vert \beta_j \vert = \text{RSS} + \lambda \sum_{j=1}^p \vert \beta_j \vert\]

The lasso: more details

• Recall that the lasso minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p\vert \beta_j \vert = \text{RSS} + \lambda \sum_{j=1}^p \vert \beta_j \vert\]

• Lasso uses an \(\ell_1\) penalty (hence also known as \(\ell_1\) regularization)

  • The \(\ell_1\) norm of a coefficient vector \(\beta\) is given by \(\displaystyle \Vert \beta \Vert_1 = \sum_{j=1}^p \vert \beta_j \vert\)

• The only difference between lasso and ridge is that ridge uses a (squared) \(\ell_2\) penalty \(\Vert \beta \Vert_2^2\), while lasso uses an \(\vert \ell_1 \vert\) penalty

• Importantly, although these two problems look relatively similar, their solutions behave very differently

The lasso: more details

• Recall that the lasso minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p\vert \beta_j \vert = \text{RSS} + \lambda \sum_{j=1}^p \vert \beta_j \vert\]

• Here, \(\lambda \ge 0\) is a tuning parameter, which controls the strength of the penalty (like ridge)

• Use cross-validation to tune \(\lambda\) (for a fixed value of \(\lambda\), lasso regression fits only a single model)

• As \(\lambda\) increases, flexibility of models decreases (bias increases, variance decreases)

  • When \(\lambda = 0\), it’s just linear regression

  • When \(\lambda \rightarrow \infty\), the coefficient estimates approach 0

  • For \(\lambda\) in between, we are balancing two ideas: fitting a linear model and shrinking the coefficients

  • But the nature of the \(\ell_1\) penalty allows some coefficients to be shrunken to zero exactly

• Lasso can handle the \(p > n\) case, i.e. more variables than observations

Shrinkage methods: lasso regression

• Lasso regression performs variable selection yielding sparse models (i.e. models that involve only a subset of the variables)

• We get different models with different number of predictors at different values of \(\lambda\)

• The coefficients shrink towards and eventually equal zero

Lasso and ridge as optimization problems

Why does the lasso, unlike ridge, result in coefficient estimates that are exactly 0?

• Lasso

\[ \underset{\beta}{\text{minimize}} \sum_{i=1}^n \left(Y_i - \beta_0 - \sum_{j=1}^p\beta_j X_{ij} \right)^2 \quad \text{subject to} \quad \sum_{j=1}^p|\beta_j| \le s \]

• Ridge

\[ \underset{\beta}{\text{minimize}} \sum_{i=1}^n \left(Y_i - \beta_0 - \sum_{j=1}^p\beta_j X_{ij} \right)^2 \quad \text{subject to} \quad \sum_{j=1}^p \beta_j ^2 \le s \]

Lasso and ridge in pictures

Lasso and ridge in pictures, explained

• Consider the case of \(p=2\) (2 predictors, hence 2 coefficients \(\beta_1\) and \(\beta_2\) to be estimated)

• The residual sum of squares has elliptical contours, centered at the unregularized least squares estimate \(\hat \beta\)

• The constraint region for lasso (left) is the diamond \(\vert \beta_1 \vert + \vert \beta_2 \vert \le s\)

• The constraint region for ridge (right) is the square \(\beta_1 ^ 2 + \beta_2 ^ 2 \le s\)

• Both methods aim to find the first point where the elliptical contours hit the constraint region

• Unlike the disk, the diamond has corners; if the solution occurs at a corner, then it has one \(\beta_j\) equal to zero

• When \(p>2\), the diamond becomes a rhomboid (with many corners, flat edges, faces, etc.), allowing more opportunities for the estimated coefficients to be zero

Elastic net

Best of both worlds: elastic net

• Motivation: when developing models, there are often strong correlations among the features

• The lasso penalty is somewhat indifferent to the choice among a set of strong but correlated features

• The ridge penalty tends to shrink the coefficients of correlated features toward each other

• The elastic net penalty is a compromise, aiming to

  • encourages highly correlated features to be average

  • encourages a sparse solution in the coefficients of these averaged features

• From the original paper’s abtract:

… the elastic net encourages a grouping effect, where strongly correlated predictors tend to be in or out of the model together.

Ridge vs lasso vs elastic net

• Ridge minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p \beta_j^2 = \text{RSS} + \lambda \sum_{j=1}^p \beta_j^2\]

• Lasso minimizes

\[\sum_{i=1}^n \big(Y_i - \beta_0 - \sum_{j=1}^p \beta_j X_{ij}\big)^2 + \lambda \sum_{j=1}^p\vert \beta_j \vert = \text{RSS} + \lambda \sum_{j=1}^p \vert \beta_j \vert\]

• Elastic net compromises between ridge and lasso

\[\sum_{i=1}^{n}\left(Y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} X_{i j}\right)^{2}+\lambda\left(\frac{1-\alpha}{2}\|\beta\|_{2}^{2}+\alpha\|\beta\|_{1} \right)\]

Elastic net: more details

• Elastic net minimizes

\[\sum_{i=1}^{n}\left(Y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} X_{i j}\right)^{2}+\lambda\left(\frac{1-\alpha}{2}\|\beta\|_{2}^{2}+\alpha\|\beta\|_{1} \right)\]

• Penalty terms: \(\lambda \cdot (1 - \alpha) / 2\) (ridge) and \(\lambda \cdot \alpha\) (lasso)

  • \(\alpha\) controls the mixing between the two types, ranges from 0 to 1

  • \(\alpha = 1\) returns lasso, \(\alpha = 0\) return ridge

• \(\lambda\) and \(\alpha\) are tuning parameters; use cross-validation to tune

Scaling of predictors

• In linear regression, the (least squares) coefficient estimates are scale equivariant

  • Multiplying \(X_j\) by a constant c simply leads to a scaling of the least squares coefficient estimates by a factor of \(1/c\)

  • i.e., regardless of how the \(j\)th predictor is scaled, \(X_j \hat \beta_j\) will remain the same

• For ridge, lasso, and elastic net: standardize the predictors

  • The coefficient estimates can change substantially when multiplying a given predictor by a constant, due to the sum of squared coefficients term in the penalty

  • For each predictor column, subtract off the mean, and divide by the standard deviation \[\tilde{x}_{ij} = \frac{x_{ij} - \bar{x}_j}{s_{x,j}}\]

Examples

Data: prostate cancer

Examine the level of a prostate specific antigen and a number of clinical measures in men who were about to receive a radical prostatectomy

library(tidyverse)
theme_set(theme_light())
# more info: https://rdrr.io/cran/ElemStatLearn/man/prostate.html
prostate <- read_tsv("https://hastie.su.domains/ElemStatLearn/datasets/prostate.data")
glimpse(prostate)

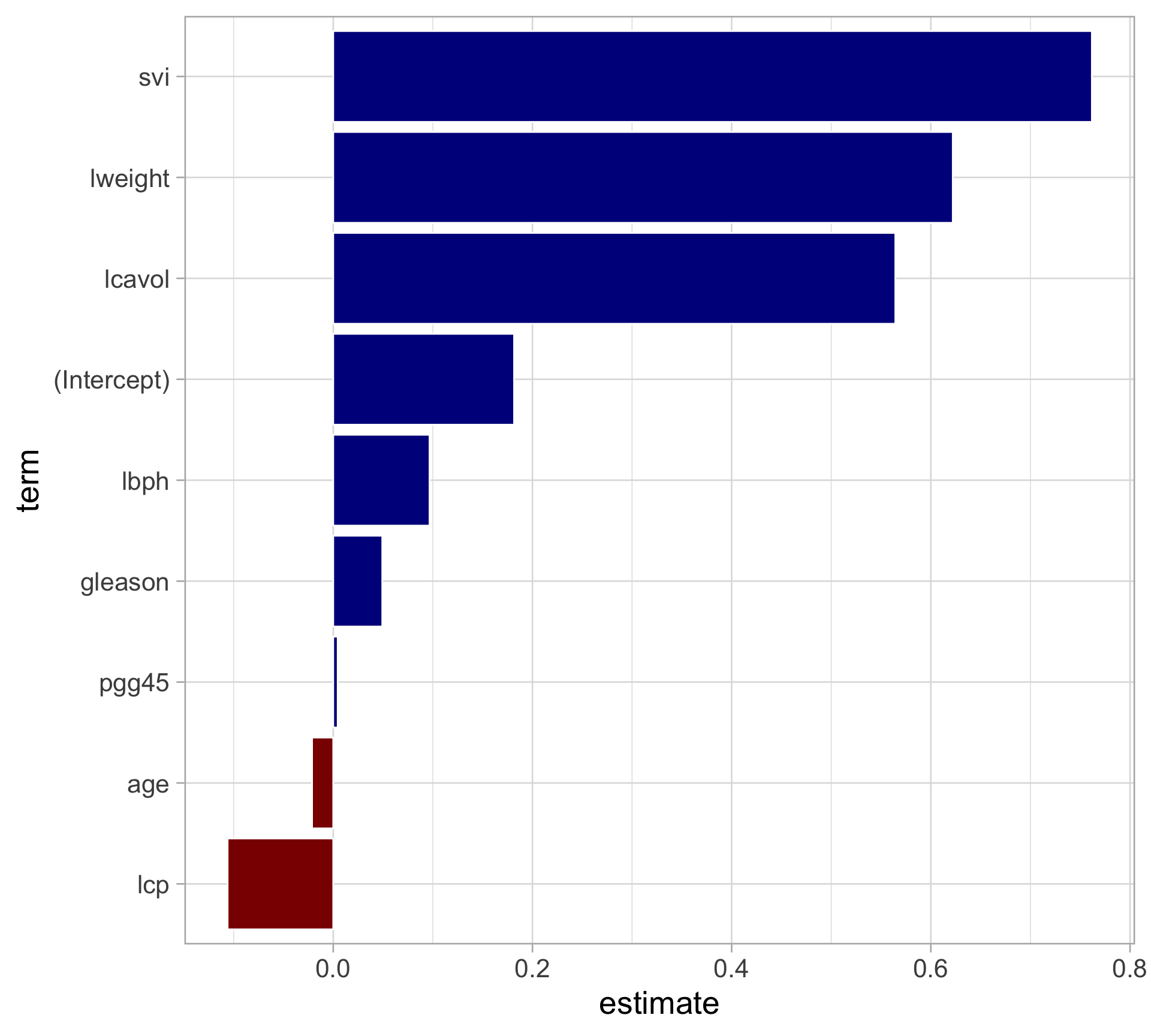
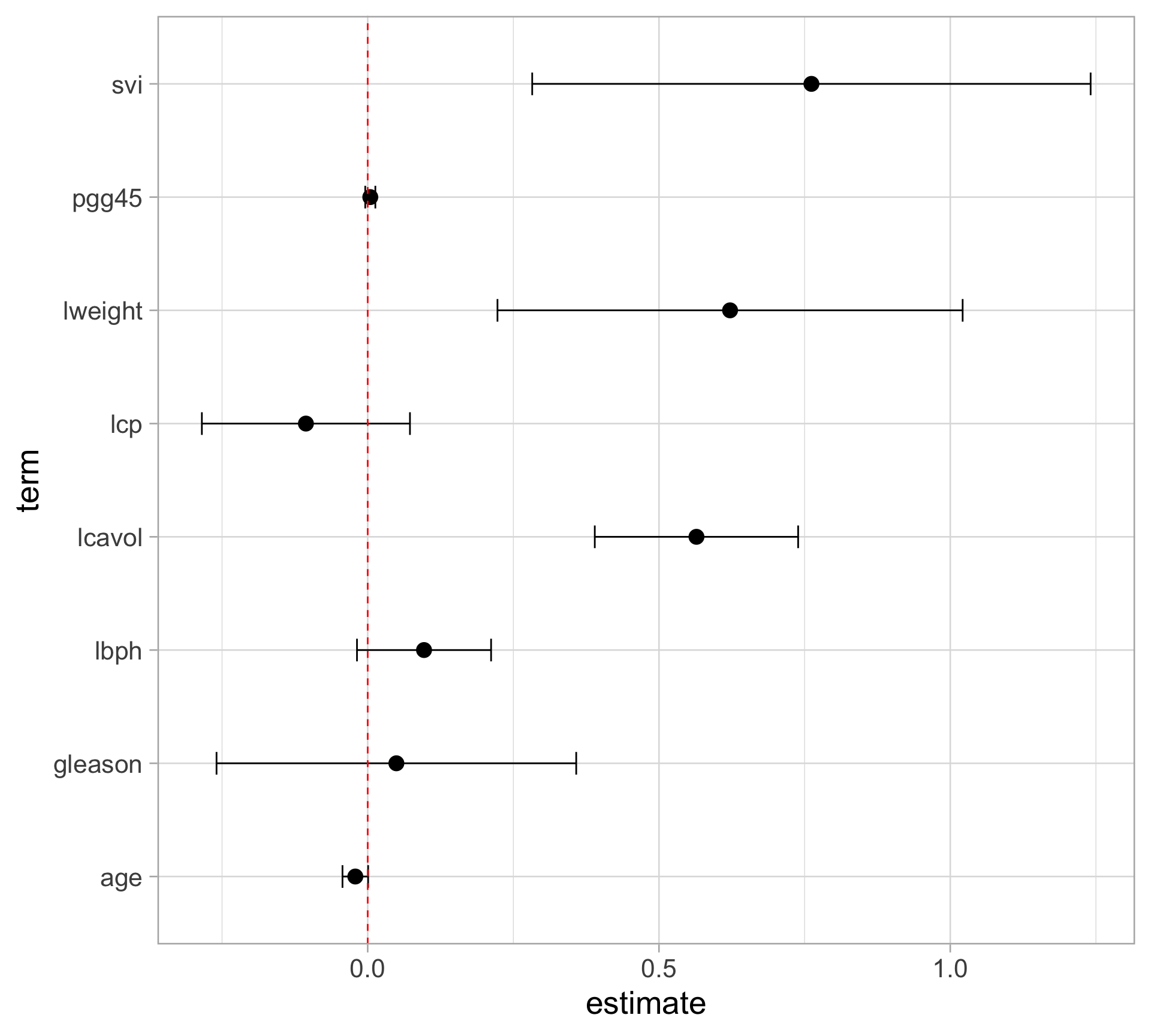
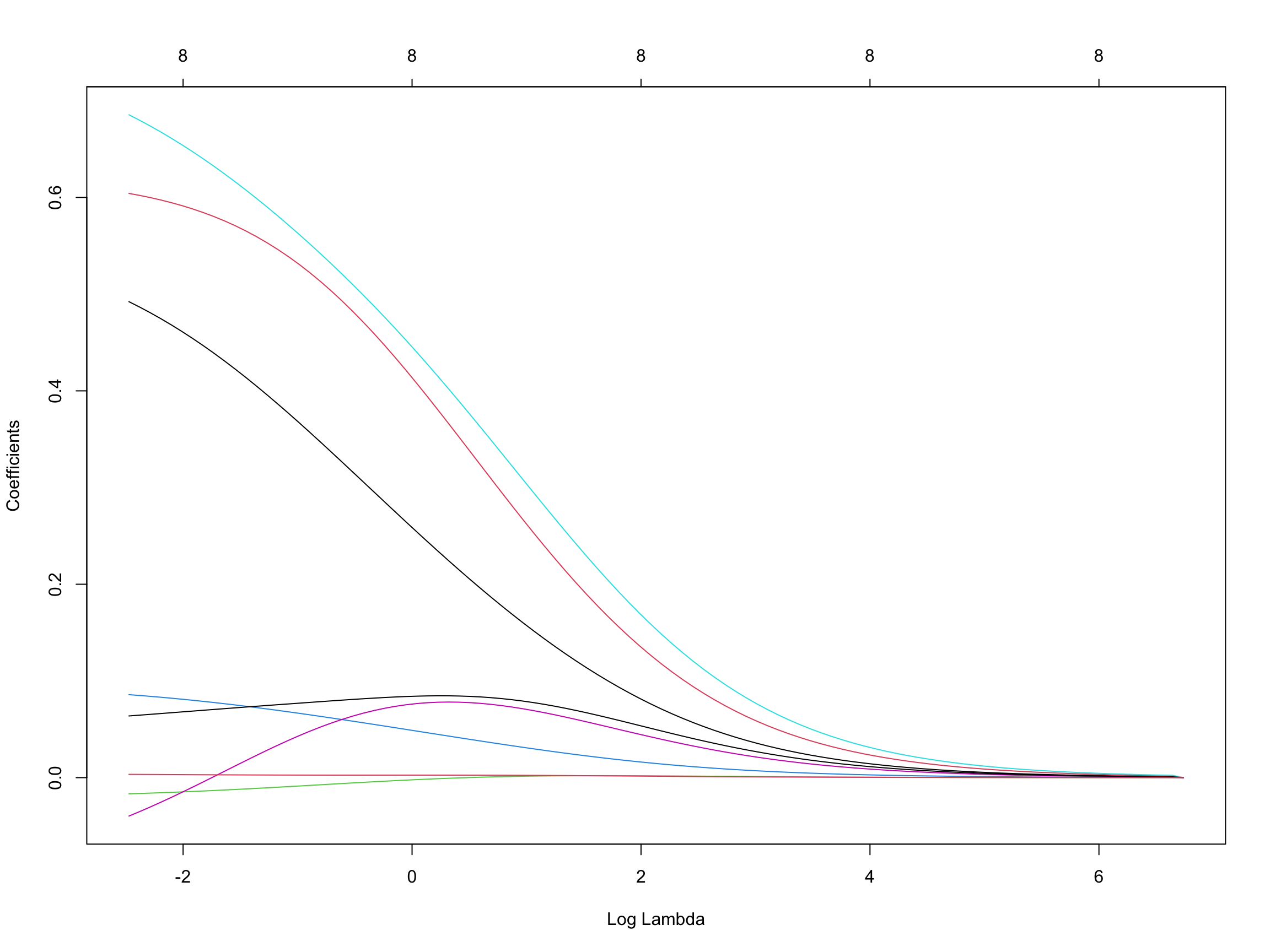
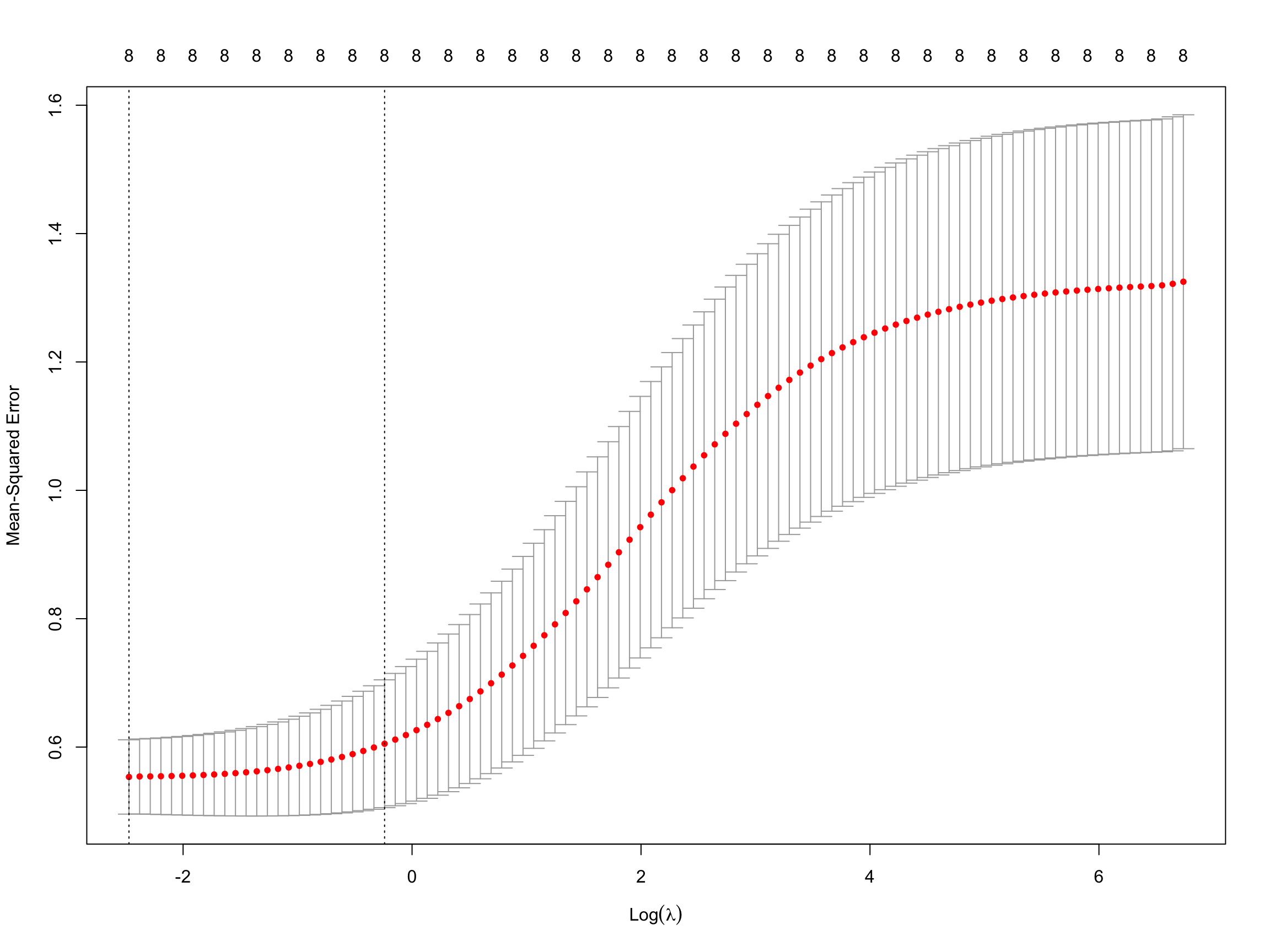
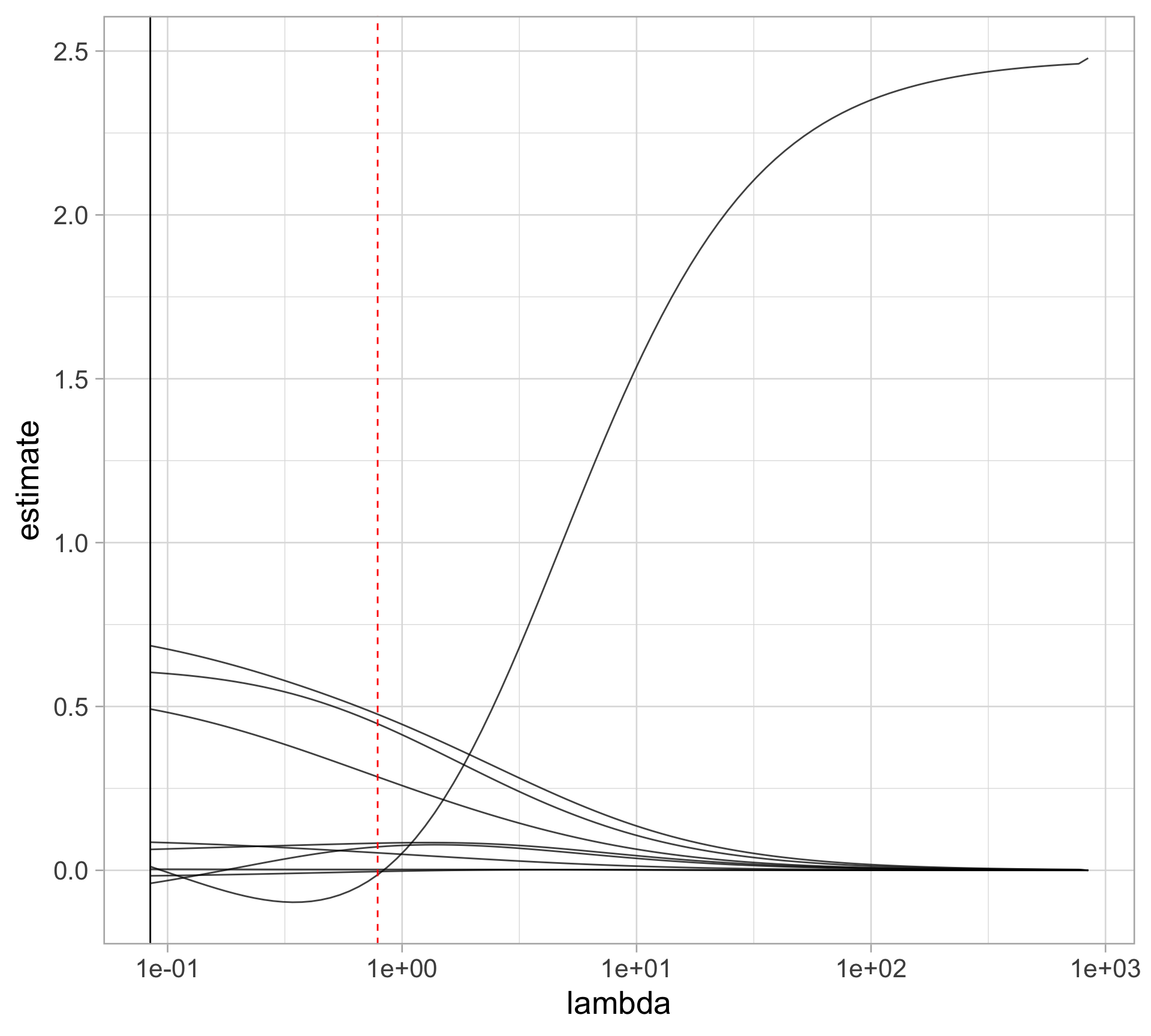
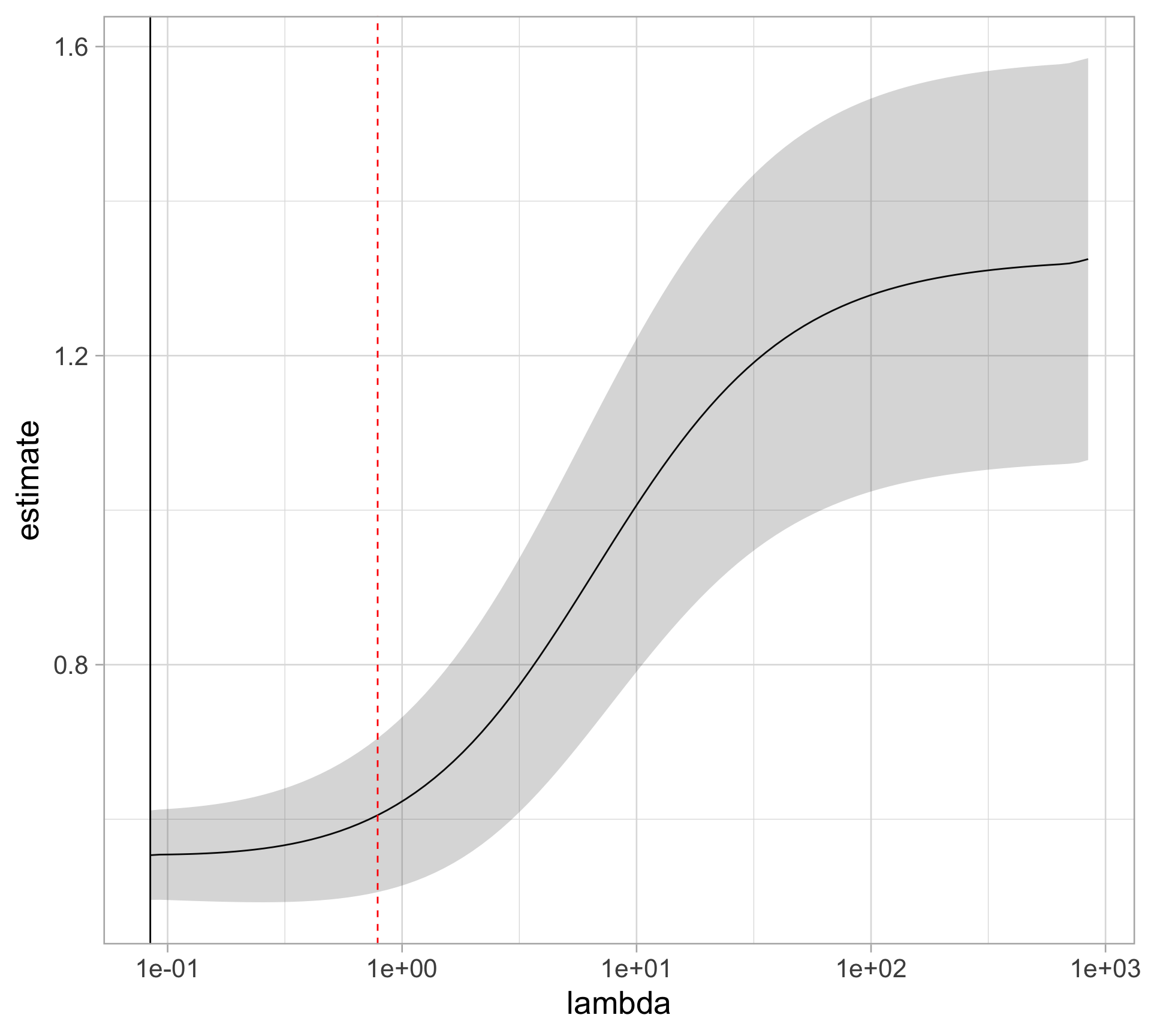
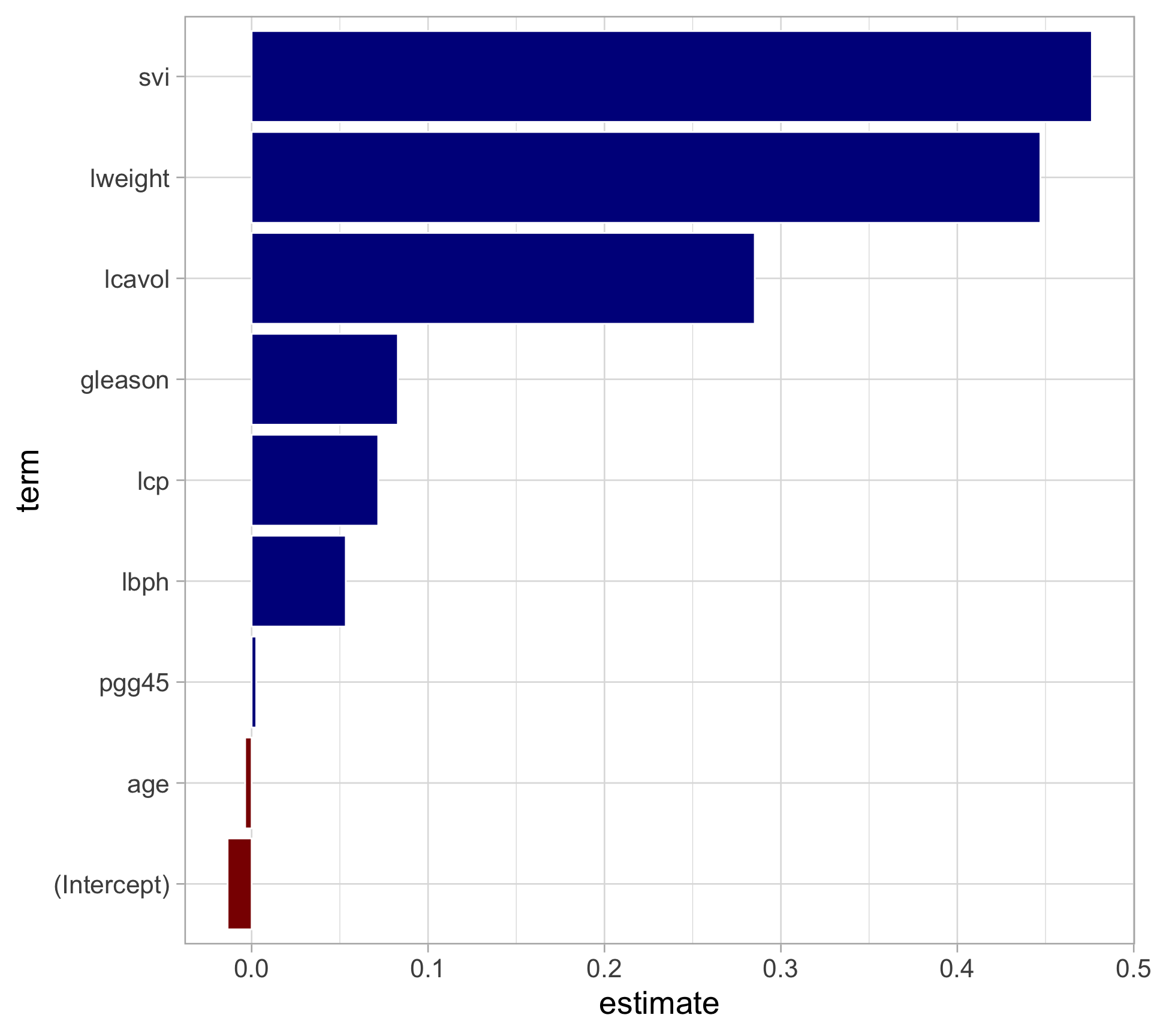
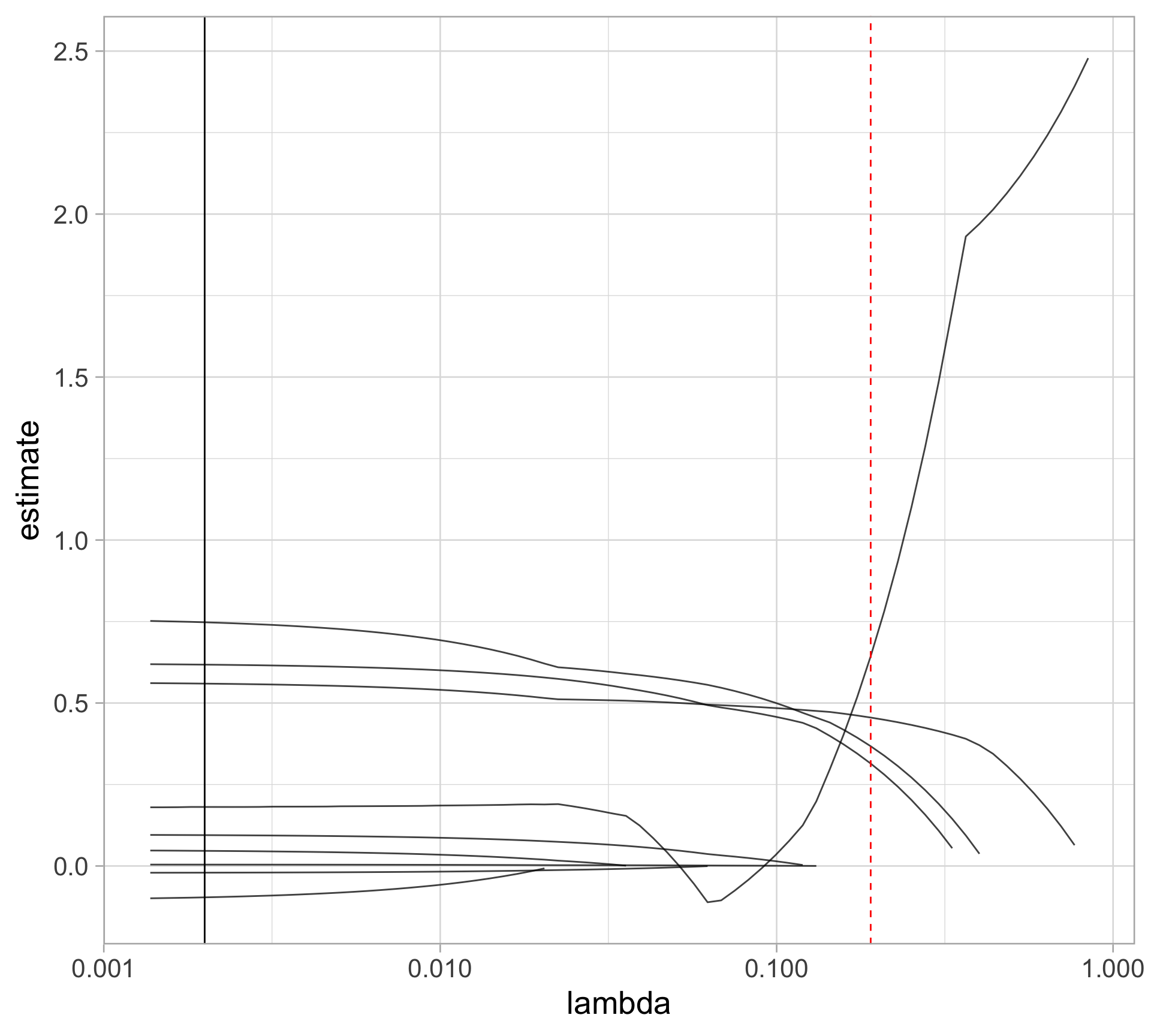
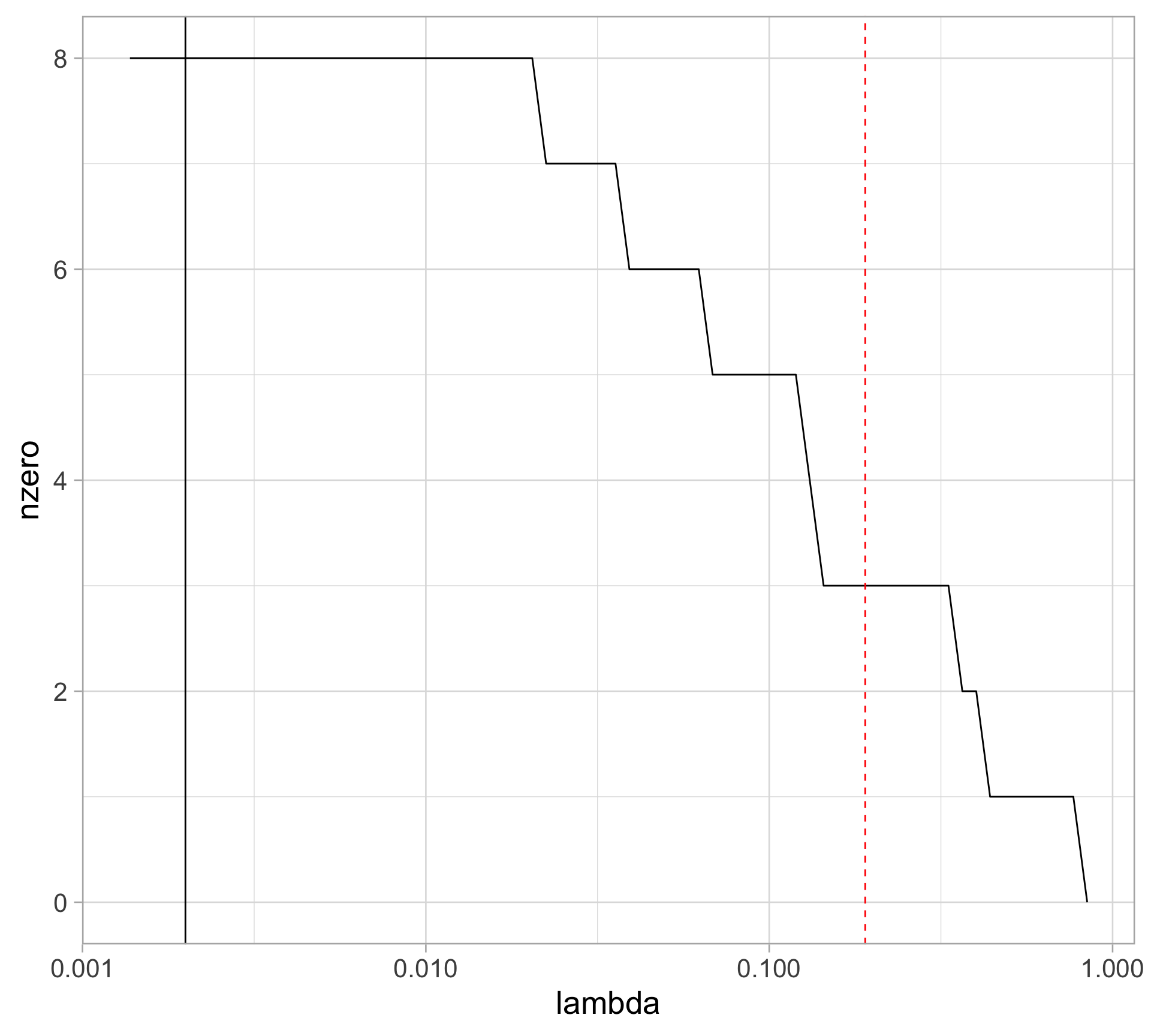
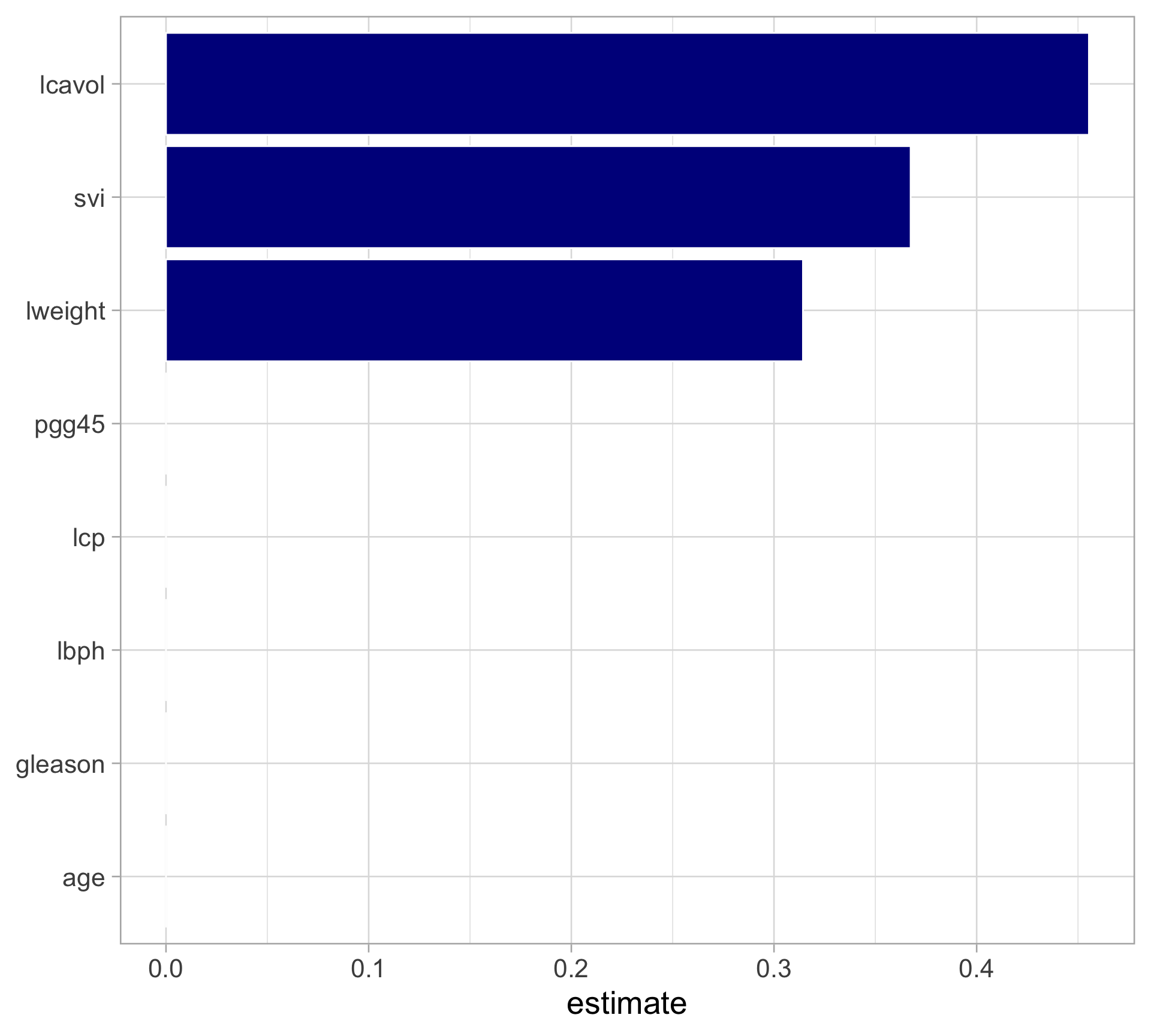
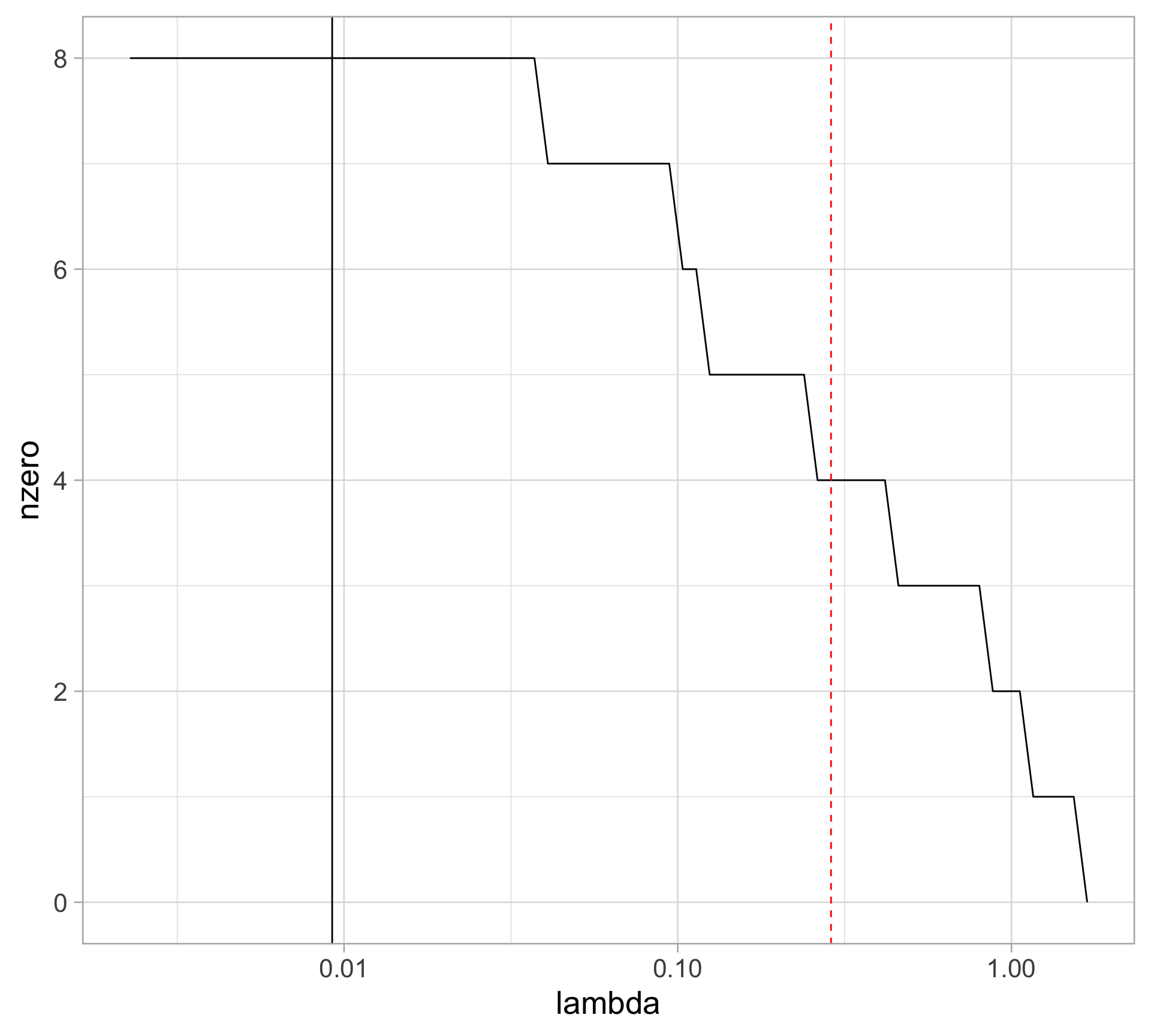
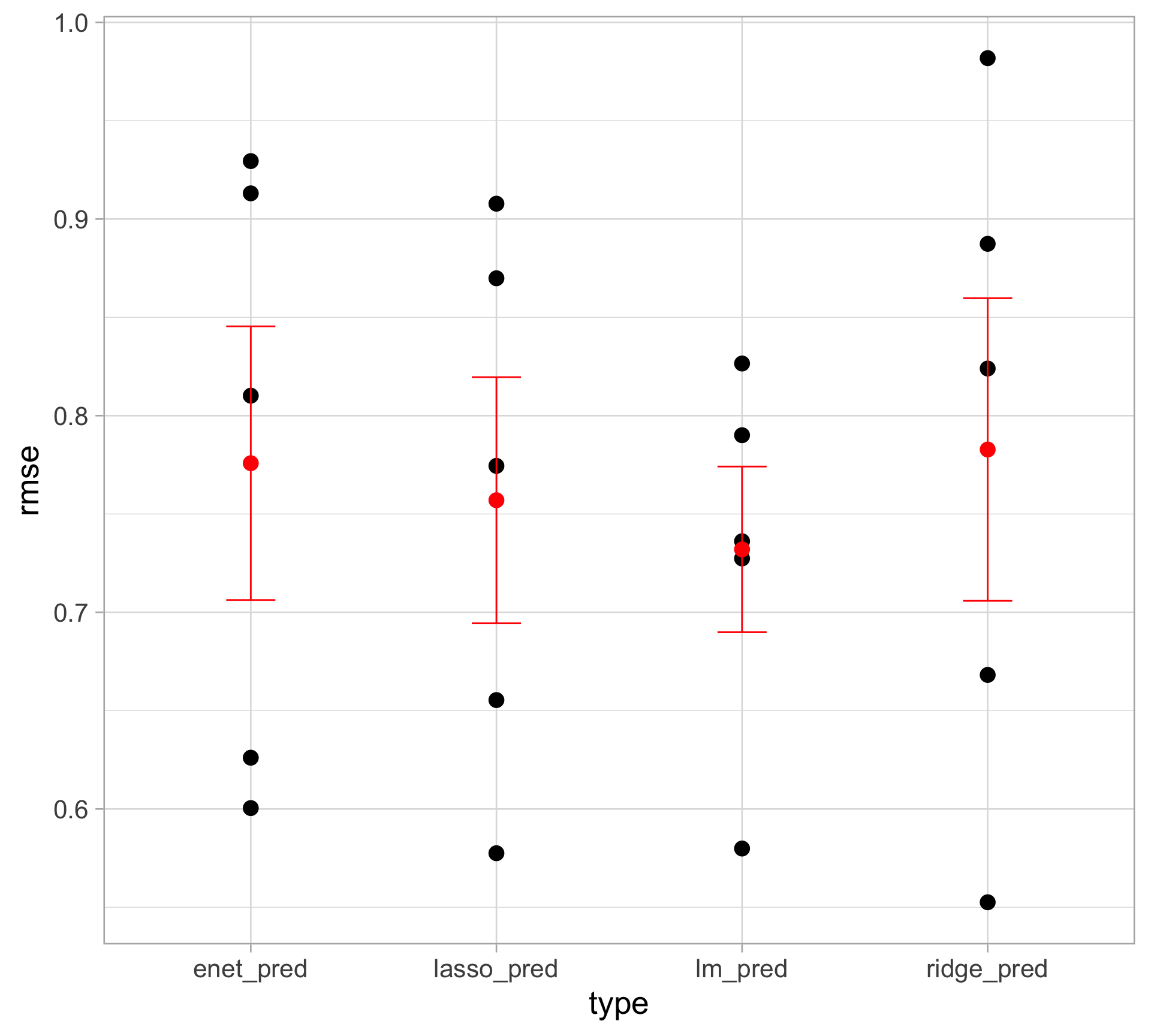
Rows: 97
Columns: 11
$ ...1    <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,…
$ lcavol  <dbl> -0.5798185, -0.9942523, -0.5108256, -1.2039728, 0.7514161, -1.…
$ lweight <dbl> 2.769459, 3.319626, 2.691243, 3.282789, 3.432373, 3.228826, 3.…
$ age     <dbl> 50, 58, 74, 58, 62, 50, 64, 58, 47, 63, 65, 63, 63, 67, 57, 66…
$ lbph    <dbl> -1.3862944, -1.3862944, -1.3862944, -1.3862944, -1.3862944, -1…
$ svi     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ lcp     <dbl> -1.3862944, -1.3862944, -1.3862944, -1.3862944, -1.3862944, -1…
$ gleason <dbl> 6, 6, 7, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 6, 7, 6, 6, 6, 6,…
$ pgg45   <dbl> 0, 0, 20, 0, 0, 0, 0, 0, 0, 0, 0, 0, 30, 5, 5, 0, 30, 0, 0, 0,…
$ lpsa    <dbl> -0.4307829, -0.1625189, -0.1625189, -0.1625189, 0.3715636, 0.7…
$ train   <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, FALSE, TRUE, FALSE, FALSE,…

Introduction to glmnet

Fit ridge, lasso, and elastic net models with glmnet

library(glmnet)
prostate <- prostate |> 
  select(lcavol:lpsa)

Create predictor matrix and response vector

# predictors
# model_x <- model.matrix(lpsa ~ ., prostate)
model_x <- prostate |> 
  select(lcavol:pgg45) |> 
  as.matrix()

# response
# model_y <- prostate$lpsa
model_y <- prostate |> 
  pull(lpsa)

Vanilla linear regression model

• What do the initial regression coefficients look like?

• Use broom to tidy model output for plotting

prostate_lm <- lm(lpsa ~ ., data = prostate)
library(broom)
prostate_lm |> 
  tidy() |> 
  mutate(term = fct_reorder(term, estimate)) |> 
  ggplot(aes(x = estimate, y = term, 
             fill = estimate > 0)) +
  geom_col(color = "white", show.legend = FALSE) +
  scale_fill_manual(values = c("darkred", "darkblue"))

Coefficient plot (w/ uncertainty)

prostate_lm |> 
  tidy(conf.int = TRUE) |> 
  filter(term != "(Intercept)") |> 
  ggplot(aes(x = estimate, y = term))  +
  geom_point(size = 4) +
  geom_errorbar(aes(xmin = conf.low, 
                    xmax = conf.high, 
                    width = 0.2)) +
  geom_vline(xintercept = 0, 
             linetype = "dashed", 
             color = "red")

Other names: dot-and-whisker plot or forest plot or blobbogram

Ridge regression

Perform ridge regression using glmnet with alpha = 0

By default, predictors are standardized and models are fitted across a range of \(\lambda\) values

prostate_ridge <- glmnet(model_x, model_y, alpha = 0)
plot(prostate_ridge, xvar = "lambda")

Ridge regression

Use cross-validation to select \(\lambda\) with cv.glmnet() which uses 10 folds by default

Specify ridge regression with alpha = 0

prostate_ridge_cv <- cv.glmnet(model_x, model_y, alpha = 0)
plot(prostate_ridge_cv)

Tidy ridge regression

# str(prostate_ridge_cv)
tidy_ridge_coef <- tidy(prostate_ridge_cv$glmnet.fit)
tidy_ridge_coef |> 
  ggplot(aes(x = lambda, y = estimate, group = term)) +
  scale_x_log10() +
  geom_line(alpha = 0.75) +
  geom_vline(xintercept = prostate_ridge_cv$lambda.min) +
  geom_vline(xintercept = prostate_ridge_cv$lambda.1se, 
             linetype = "dashed", color = "red")

• Could easily add color with legend for variables…

Tidy ridge regression

tidy_ridge_cv <- tidy(prostate_ridge_cv)
tidy_ridge_cv |> 
  ggplot(aes(x = lambda, y = estimate)) +
  geom_line() + 
  scale_x_log10() +
  geom_ribbon(aes(ymin = conf.low, ymax = conf.high), 
              alpha = 0.2) +
  geom_vline(xintercept = prostate_ridge_cv$lambda.min) +
  geom_vline(xintercept = prostate_ridge_cv$lambda.1se,
             linetype = "dashed", color = "red")

Ridge regression coefficients

Coefficients using the one-standard-error rule

(select the model with estimated test error within 1 SE of the minimum test error)

# ridge_final <- glmnet(
#   model_x, model_y, alpha = 0,
#   lambda = prostate_ridge_cv$lambda.1se,
# )
# library(vip)
# ridge_final |> 
#   vip()

tidy_ridge_coef |>
  filter(lambda == prostate_ridge_cv$lambda.1se) |>
  mutate(term = fct_reorder(term, estimate)) |>
  ggplot(aes(x = estimate, y = term, 
             fill = estimate > 0)) +
  geom_col(color = "white", show.legend = FALSE) +
  scale_fill_manual(values = c("darkred", "darkblue"))

Lasso regression example

Similar syntax to ridge but specify alpha = 1:

prostate_lasso_cv <- cv.glmnet(model_x, model_y, 
                               alpha = 1)
tidy_lasso_coef <- tidy(prostate_lasso_cv$glmnet.fit)
tidy_lasso_coef |> 
  ggplot(aes(x = lambda, y = estimate, group = term)) +
  scale_x_log10() +
  geom_line(alpha = 0.75) +
  geom_vline(xintercept = prostate_lasso_cv$lambda.min) +
  geom_vline(xintercept = prostate_lasso_cv$lambda.1se, 
             linetype = "dashed", color = "red")

Lasso regression example

Number of non-zero predictors by \(\lambda\)

tidy_lasso_cv <- tidy(prostate_lasso_cv)
tidy_lasso_cv |>
  ggplot(aes(x = lambda, y = nzero)) +
  geom_line() +
  geom_vline(xintercept = prostate_lasso_cv$lambda.min) +
  geom_vline(xintercept = prostate_lasso_cv$lambda.1se, 
             linetype = "dashed", color = "red") +
  scale_x_log10()

Reduction in variables using one-standard-error rule

Lasso regression example

Coefficients using the one-standard-error rule

# this will only print out non-zero coefficient estimates
# tidy_lasso_coef |>
#   filter(lambda == prostate_lasso_cv$lambda.1se)

lasso_final <- glmnet(
  model_x, model_y, 
  alpha = 1,
  lambda = prostate_lasso_cv$lambda.1se,
)
library(vip)
lasso_final |> 
  vi() |> 
  mutate(Variable = fct_reorder(Variable, Importance)) |>
  ggplot(aes(x = Importance, y = Variable, 
             fill = Importance > 0)) +
  geom_col(color = "white", show.legend = FALSE) +
  scale_fill_manual(values = c("darkred", "darkblue")) +
  labs(x = "estimate", y = NULL)

Elastic net example

Need to tune both \(\lambda\) and \(\alpha\) - can do so manually with our own folds

set.seed(100)
fold_id <- sample(rep(1:10, length.out = nrow(model_x)))

Then use cross-validation with these folds for different candidate alpha values:

cv_enet_25 <- cv.glmnet(model_x, model_y, foldid = fold_id, alpha = 0.25)
cv_enet_50 <- cv.glmnet(model_x, model_y, foldid = fold_id, alpha = 0.5)
cv_ridge <- cv.glmnet(model_x, model_y, foldid = fold_id, alpha = 0)
cv_lasso <- cv.glmnet(model_x, model_y, foldid = fold_id, alpha = 1)

Can see which one had the lowest CV error among its candidate \(\lambda\) values:

which.min(c(min(cv_enet_25$cvm), min(cv_enet_50$cvm), min(cv_ridge$cvm), min(cv_lasso$cvm)))

[1] 3

Elastic net example

Can view same type of summary

cv_enet_50 |> 
  tidy() |> 
  ggplot(aes(x = lambda, y = nzero)) +
  geom_line() +
  geom_vline(xintercept = cv_enet_50$lambda.min) +
  geom_vline(xintercept = cv_enet_50$lambda.1se, 
             linetype = "dashed", 
             color = "red") +
  scale_x_log10()

• More relaxed than lasso for variable entry

Comparison of models based on holdout performance

set.seed(101)
N_FOLDS <- 5
prostate <- prostate |>
  mutate(test_fold = sample(rep(1:N_FOLDS, length.out = n())))

get_test_pred <- function(x) {
  test_data <- prostate |> filter(test_fold == x)                     # get test and training data
  train_data <- prostate |> filter(test_fold != x)
  test_x <- as.matrix(select(test_data, -lpsa))                       # get test and training matrices
  train_x <- as.matrix(select(train_data, -lpsa))
  
  lm_fit <- lm(lpsa ~ ., data = train_data)                           # fit models to training data
  ridge_fit <- cv.glmnet(train_x, train_data$lpsa, alpha = 0)
  lasso_fit <- cv.glmnet(train_x, train_data$lpsa, alpha = 1)
  enet_fit <- cv.glmnet(train_x, train_data$lpsa, alpha = 0.5)
  
  tibble(lm_pred = predict(lm_fit, newdata = test_data),              # return test results
         ridge_pred = as.numeric(predict(ridge_fit, newx = test_x)),
         lasso_pred = as.numeric(predict(lasso_fit, newx = test_x)),
         enet_pred = as.numeric(predict(enet_fit, newx = test_x)),
         test_actual = test_data$lpsa,
         test_fold = x)
}

test_pred_all <- map(1:N_FOLDS, get_test_pred) |> 
  bind_rows()

Comparison of models based on holdout performance

Compute RMSE across folds with standard error intervals

test_pred_all |>
  pivot_longer(lm_pred:enet_pred, 
               names_to = "type", 
               values_to = "test_pred") |>
  group_by(type, test_fold) |>
  summarize(
    rmse = sqrt(mean((test_actual - test_pred)^2))
  ) |> 
  ggplot(aes(x = type, y = rmse)) + 
  geom_point(size = 4) +
  stat_summary(fun = mean, geom = "point", 
               color = "red", size = 4) + 
  stat_summary(fun.data = mean_se, geom = "errorbar", 
               color = "red", width = 0.2)

Linear regression actually slightly outperforms regularization here, but within intervals